C - +/- Rectangle Editorial /

Time Limit: 2 sec / Memory Limit: 256 MB

配点 : 700 点

問題文

整数 H, W, h, w (1 ≤ h ≤ H, 1 ≤ w ≤ W) が与えられます。 次の条件がすべて成り立つような行列が存在するか判定し、存在するならばひとつ構成してください。

  • 行列は H 行 W 列である。
  • 行列の各要素は -10^9 以上 10^9 以下の整数である。
  • 行列の全要素の総和は正の値である。
  • どこから h 行 w 列の部分長方形を取り出しても、部分長方形に含まれる全要素の総和は負の値である。

制約

  • 1 ≤ h ≤ H ≤ 500
  • 1 ≤ w ≤ W ≤ 500

入力

入力は以下の形式で標準入力から与えられる。

H W h w

出力

条件がすべて成り立つような行列が存在しないならば、No を出力せよ。

存在するならば、1 行目に Yes を出力し、2 行目以降に行列をひとつ出力せよ。 行列は以下の形式で出力せよ。 ただし、a_{ij} は行列の (i,\ j) 要素を表す。

a_{11} ... a_{1W}
:
a_{H1} ... a_{HW}

入力例 1

3 3 2 2

出力例 1

Yes
1 1 1
1 -4 1
1 1 1

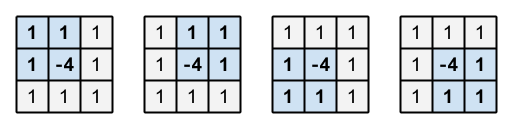
行列の全要素の総和は 4 であり、正の値です。 また、部分長方形を取り出す方法は次図の 4 通りですが、どの場合も、部分長方形に含まれる全要素の総和は -1 であり、負の値です。

bbdb651fa1f05996886da9f0c4d8090a.png

入力例 2

2 4 1 2

出力例 2

No

入力例 3

3 4 2 3

出力例 3

Yes
2 -5 8 7
3 -5 -4 -5
2 1 -1 7

Score : 700 points

Problem Statement

You are given four integers: H, W, h and w (1 ≤ h ≤ H, 1 ≤ w ≤ W). Determine whether there exists a matrix such that all of the following conditions are held, and construct one such matrix if the answer is positive:

  • The matrix has H rows and W columns.
  • Each element of the matrix is an integer between -10^9 and 10^9 (inclusive).
  • The sum of all the elements of the matrix is positive.
  • The sum of all the elements within every subrectangle with h rows and w columns in the matrix is negative.

Constraints

  • 1 ≤ h ≤ H ≤ 500
  • 1 ≤ w ≤ W ≤ 500

Input

Input is given from Standard Input in the following format:

H W h w

Output

If there does not exist a matrix that satisfies all of the conditions, print No.

Otherwise, print Yes in the first line, and print a matrix in the subsequent lines in the following format:

a_{11} ... a_{1W}
:
a_{H1} ... a_{HW}

Here, a_{ij} represents the (i,\ j) element of the matrix.

Sample Input 1

3 3 2 2

Sample Output 1

Yes
1 1 1
1 -4 1
1 1 1

The sum of all the elements of this matrix is 4, which is positive. Also, in this matrix, there are four subrectangles with 2 rows and 2 columns as shown below. For each of them, the sum of all the elements inside is -1, which is negative.

bbdb651fa1f05996886da9f0c4d8090a.png

Sample Input 2

2 4 1 2

Sample Output 2

No

Sample Input 3

3 4 2 3

Sample Output 3

Yes
2 -5 8 7
3 -5 -4 -5
2 1 -1 7