A - 2点間距離の最大値 ( The longest distance )
Editorial
 /
/ 
平面上に N 個の点があり、それぞれ 0 から N-1 までの番号が付けられており、それぞれの点について x 座標と y 座標が与えられています。
その N 点のうち 2 点を選び結んで得られる線分のうち、最も長くなる線分の長さを求めてください。
入力は以下の形式で標準入力から与えられる。
N 点のうち 2 点を選び結んで得られる線分のうち、最も長い線分の長さを標準出力に 1 行で出力せよ。
誤差は絶対誤差あるいは相対誤差の少なくとも片方が 10^{-3} 以下であれば許容する。
なお、最後には改行を出力せよ。
 /
/ 
Time Limit: 2 sec / Memory Limit: 64 MB
問題文
その N 点のうち 2 点を選び結んで得られる線分のうち、最も長くなる線分の長さを求めてください。
入力
N
x_{0} y_{0}
x_{1} y_{1}
:
:
x_{N-1} y_{N-1}
- 入力は N+1 行ある。
- 1 行目には、点の個数を表す整数 N (2≦N≦100)が与えられる。
- 2 行目から N+1 行目までの i+2 (0 ≦ i < N) 行目には、i 番の点の x 座標を表す整数 x_{i}(0≦x_{i}≦100) と y 座標を表す整数 y_{i}(0≦y_{i}≦100) が空白を区切りとして与えられる。
- 与えられる点のうち x 座標と y 座標がともに一致する点の組は存在しないが、2 つの点を繋ぐ線分上に他の点が存在することはありうる。
出力
誤差は絶対誤差あるいは相対誤差の少なくとも片方が 10^{-3} 以下であれば許容する。
なお、最後には改行を出力せよ。
入力例 1
3 1 1 2 4 4 3
出力例 1
3.605551
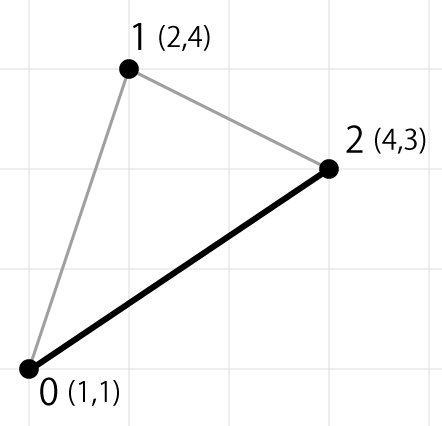
- 3 点の位置関係を示すと下図のようになります。

- (1,1) と (2,4) を繋いだ線分の長さは \sqrt{(2-1)^2+(4-1)^2} = \sqrt{10} = 3.162278 です。
- (2,4) と (4,3) を繋いだ線分の長さは \sqrt{(4-2)^2+(3-4)^2} = \sqrt{5} = 2.236068 です。
- (4,3) と (1,1) を繋いだ線分の長さは \sqrt{(1-4)^2+(1-3)^2} = \sqrt{13} = 3.605551 です。
- 以上により最も長い線分の長さは太線が示す 3.605551 になります。
入力例 2
10 1 8 4 0 3 7 2 4 5 9 9 1 6 2 0 2 8 6 7 8
出力例 2
10.630146
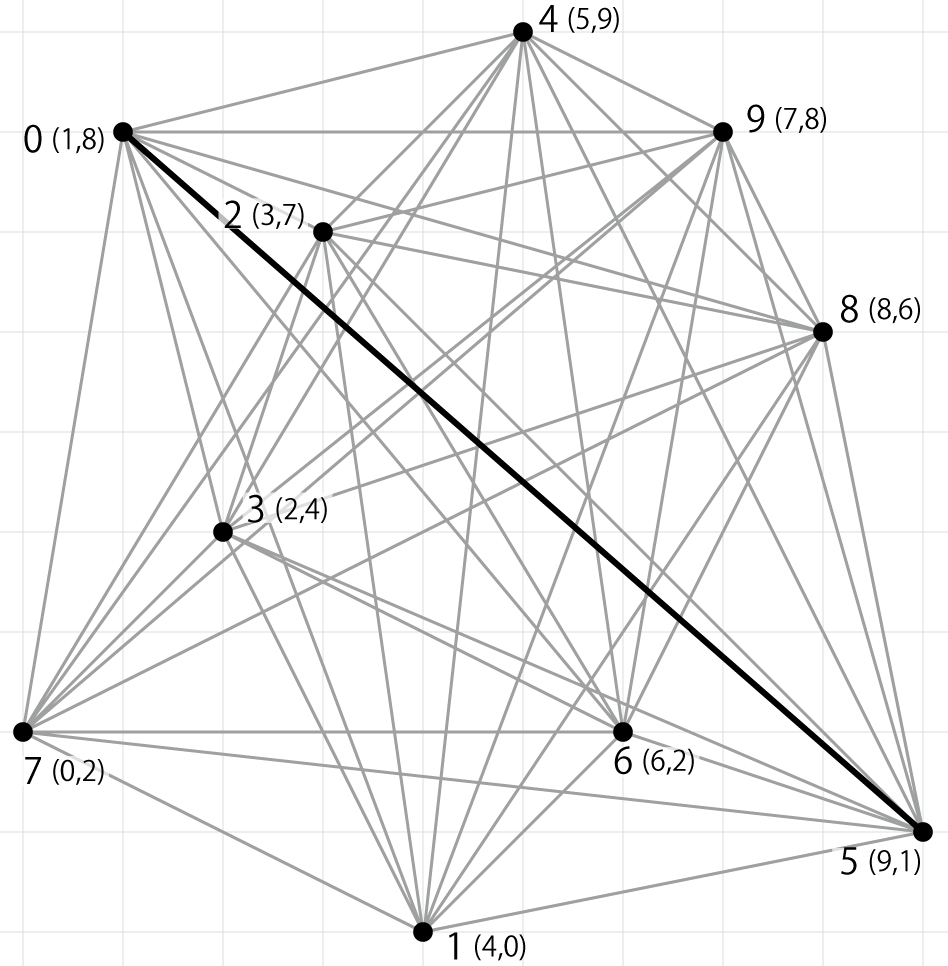
- 10 点の位置関係を示すと下図のようになります。
- 最も長い線分は点 0 と点 5 を繋ぐ線分で、10.630146 になります。

入力例 3
4 0 0 0 100 100 0 100 100
出力例 3
141.421356
- 最も長い線分は点 0 と点 3 を繋ぐ線分、または点 1 と点 2 を繋ぐ線分で、141.421356 になります。
入力例 4
5 3 0 1 0 0 0 4 0 2 0
出力例 4
4.000000
- 最も長い線分は点 2 と点 3 を繋ぐ線分で、その長さは 4.000000 です。
入力例 5
4 2 2 0 0 1 1 3 3
出力例 5
4.242641
- 最も長い線分は点 1 と点 3 を繋ぐ線分で、その長さは 4.242641 です。