 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
問題文
多橋君は橋が大好きです。したがって、全ての辺が橋(グラフ理論用語)となる木と呼ばれるグラフが大好きです。また、多橋君は最近学校でXORについて学びました。そこで、次のような問題について考えています。
N 頂点と N-1 本の辺からなる連結な無向グラフ、つまり木が与えられます。各頂点は、それぞれ頂点 1、頂点 2、…、頂点 N と呼ばれます。各辺にはそれぞれ非負整数のコストが割り振られています。
整数 X が与えられるので、頂点 a と頂点 b を結ぶ単純パス(同じ辺を二度通らないパス、木においては必ず 1 つだけ存在する)上の辺のコストの\rm{xor}和が X になるような組 (a,b) (1≦a<b≦N)の総数を求めてください。 ただし\rm{xor}和とは、いくつかの整数 A_1,A_2,… があったとき、それらの2進表現のビット毎の排他的論理和 A_1 \rm{xor} A_2 \rm{xor}… により得られる値のことを表します。 例えば、1 \rm{xor} 2 \rm{xor} 5 は 6 です。
あなたの仕事は、多橋君の代わりにこの問題を解くことです。
入力
入力は以下の形式で標準入力から与えられる。
N X
x_1 y_1 c_1
x_2 y_2 c_2
:
x_{N-1} y_{N-1} c_{N-1}
- 1 行目には、グラフの頂点数を表す整数 N (1 ≦ N ≦ 100,000) と問題文中の整数 X (0≦X≦10^9) が与えられる。
- 続く N-1 行には、グラフの N-1 本の辺の情報が与えられる。このうち i(1≦i≦N-1) 行目には、i 番目の辺が結ぶ 2 つの頂点 x_i,y_i(1≦x_i,y_i≦N) とコスト c_i (0≦c_i≦10^9) が与えられる。
- 与えられるグラフは連結であることが保証される。
出力
1 行目に問題文中で求められている答えを出力せよ。末尾に改行を入れること。
入力例1
6 7 1 2 5 2 3 3 3 4 6 2 5 2 5 6 7
出力例1
3
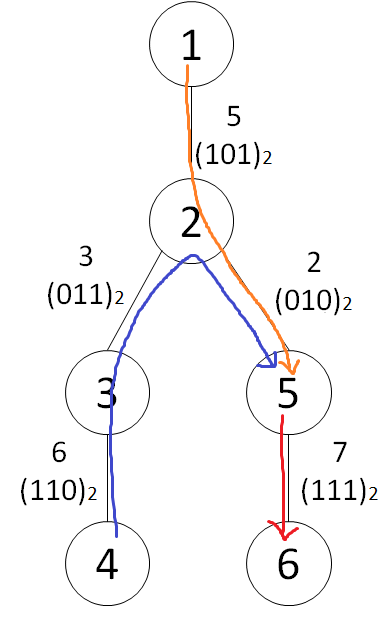
(a,b)=(1,5),(4,5),(5,6) のとき、パス上の辺のコストの\rm{xor}和が 7(2進表記で111) となるので答えは 3 となる。
この入力例に対するグラフは下図のようになる。コストについては、その10進表記と2進表記を表示している。
入力例2
6 3 1 2 1 2 3 3 3 4 2 4 5 3 4 6 1
出力例2
4
入力例3
10 1 9 10 1 6 10 1 5 2 1 8 6 1 4 5 1 7 6 0 3 8 0 3 1 1 8 2 0
出力例3
25