 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 700 点
問題文
H \times W のマス目があります.
マス目の各マスは黒か白かに塗られており,上から i 番目,左から j 番目のマスは,S_i の j 文字目が # のとき黒マス,. のとき白マスです.
すぬけ君は,マス目に対して次の操作を好きな回数行うことができます.
- マス目の任意の行または列を選び,その行または列のすべてのマスの色を反転する (すなわち,黒で塗られたマスを白に,白で塗られたマスを黒に塗り替える).
操作の後,すぬけ君はマス目に沿った長方形を 1 個選びます.このとき,選んだ長方形に含まれるすべてのマスは黒で塗られていなければなりません.
うまく操作を行うとき,すぬけ君が選ぶことができる最大の長方形の面積を求めてください.
制約
- 2 \leq H \leq 2000
- 2 \leq W \leq 2000
- |S_i| = W
- S_i は
#,.のみからなる.
入力
入力は以下の形式で標準入力から与えられる。
H W S_1 S_2 : S_H
出力
すぬけ君が選ぶことができる最大の長方形の面積を出力せよ.
入力例 1
3 3 ..# ##. .#.
出力例 1
6
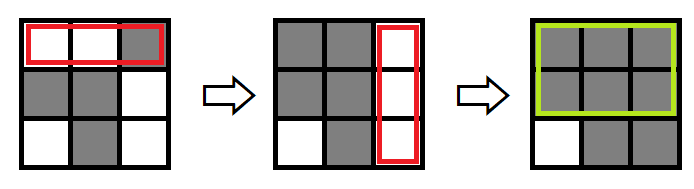
下図のように,上から 1 行目,左から 3 列目を反転させると,2 \times 3 の長方形を選ぶことができます.
入力例 2
4 4 .... .... .... ....
出力例 2
16
入力例 3
10 8 ##...#.# ##...#.# ..###.#. #.##.#.# .#..#.#. ..##.#.# ##.#.#.. ...#.#.. ###.#.## ###..###
出力例 3
27
Score : 700 points
Problem Statement
We have a board with an H \times W grid.
Each square in the grid is painted in black or white. The square at the i-th row from the top and j-th column from the left is black if the j-th character in S_i is #, and white if that character is ..
Snuke can perform the following operation on the grid any number of times:
- Select a row or column in the grid, and invert the color of all the squares in that row or column (that is, black squares become white and vice versa).
Then, Snuke draws a rectangle along grid lines. Here, all the squares contained in the rectangle must be painted in black.
Find the maximum possible area of Snuke's rectangle when the operation is performed optimally.
Constraints
- 2 \leq H \leq 2000
- 2 \leq W \leq 2000
- |S_i| = W
- S_i consists of
#and..
Input
Input is given from Standard Input in the following format:
H W S_1 S_2 : S_H
Output
Print the maximum possible area of Snuke's rectangle.
Sample Input 1
3 3 ..# ##. .#.
Sample Output 1
6
If the first row from the top and the third column from the left are inverted, a 2 \times 3 rectangle can be drawn, as shown below:

Sample Input 2
4 4 .... .... .... ....
Sample Output 2
16
Sample Input 3
10 8 ##...#.# ##...#.# ..###.#. #.##.#.# .#..#.#. ..##.#.# ##.#.#.. ...#.#.. ###.#.## ###..###
Sample Output 3
27