Time Limit: 2 sec / Memory Limit: 1024 MB
配点 : 300 点
問題文
整数 N,K が与えられます。 N を、3^m (m は非負整数)の形の数をちょうど K 個用いた和として表すことは可能でしょうか。 すなわち、
N= 3^{m_1}+3^{m_2}+...+3^{m_K}
となるような非負整数の列 (m_1, m_2,\ldots , m_K) が存在するでしょうか。
T 個のテストケースが与えられるので、それぞれについて答えてください。
制約
- 1 \leq T \leq 10^5
- 1 \leq K \leq N \leq 10^{18}
- 入力される値はすべて整数である
入力
入力は以下の形式で標準入力から与えられる。
T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
各テストケース \mathrm{case}_i (1\leq i \leq T) は以下の形式である。
N K
出力
T 行出力せよ。i 行目には、i 番目のテストケースについて、題意の非負整数の列が存在する場合は Yes を、そうでない場合は No を出力せよ。
入力例 1
4 5 3 17 2 163 79 1000000000000000000 1000000000000000000
出力例 1
Yes No Yes Yes
1 つめのテストケースについて、 5=3^1+3^0+3^0 と表すことができるため、題意の条件を満たしています。
2 つめのテストケースについて、17=3^{m_1}+3^{m_2} となる非負整数の列 (m_1, m_2) は存在しないため、題意の条件を満たしていません。
Score : 300 points
Problem Statement
You are given integers N and K. Is it possible to express N as the sum of exactly K numbers of the form 3^m (m is a non-negative integer)? In other words, is there a sequence of non-negative integers (m_1, m_2,\ldots, m_K) such that:
N= 3^{m_1}+3^{m_2}+...+3^{m_K}?
You are given T test cases. Answer each of them.
Constraints
- 1 \leq T \leq 10^5
- 1 \leq K \leq N \leq 10^{18}
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
Each test case, \mathrm{case}_i (1\leq i \leq T), is in the following format:
N K
Output
Print T lines. The i-th line should contain Yes if there is a sought sequence of non-negative integers for the i-th test case, and No otherwise.
Sample Input 1
4 5 3 17 2 163 79 1000000000000000000 1000000000000000000
Sample Output 1
Yes No Yes Yes
For the first test case, we have 5=3^1+3^0+3^0, so the condition in question is satisfied.
For the second test case, there is no sequence of non-negative integers (m_1, m_2) such that 17=3^{m_1}+3^{m_2}, so the condition in question is not satisfied.
Time Limit: 2 sec / Memory Limit: 1024 MB
配点 : 500 点
問題文
頂点に 1 から N までの番号がついた N 頂点の単純、連結な無向グラフがあります。 このグラフには M 本の辺があり、 i 番目の辺は 2 頂点 a_i , b_i を結んでいます。
また、各頂点は白または黒の色を持ち、最初の状態が c_i で与えられます。 c_i は 0 または 1 であり、c_i=0 であれば頂点 i は初め白色であり、c_i=1 であれば頂点 i は初め黒色です。
あなたはこのグラフ上で、好きな頂点を 1 つ選んで出発点とし、
- 今いる頂点と辺で結ばれた頂点のうち、今いる頂点と異なる色の頂点に移動する。その直後に、移動元の頂点の色を反転する(元の色が白なら黒に、黒なら白に変える)。
という動作を好きな回数繰り返します。
1 回以上の動作を行ったうえで、再び出発点に戻ってくることは可能でしょうか。
制約
- 2 \leq N \leq 2 \times 10^5
- N-1 \leq M \leq \mathrm{min} \lbrace 2 \times 10^5,N(N-1)/2 \rbrace
- 1 \leq a_i, b_i \leq N (1 \leq i \leq M)
- c_i=0 または c_i=1 (1 \leq i \leq N)
- 与えられるグラフは単純かつ連結である
- 入力される値はすべて整数である
入力
入力は以下の形式で標準入力から与えられる。
N M a_1 b_1 a_2 b_2 \vdots a_M b_M c_1 c_2 \ldots c_N
出力
1 回以上の動作を行ったうえで再び出発点に戻ってくることが可能な場合は Yes を、そのようなことが不可能な場合は No を出力せよ。
入力例 1
4 4 1 2 2 3 3 4 4 2 0 1 0 1
出力例 1
Yes
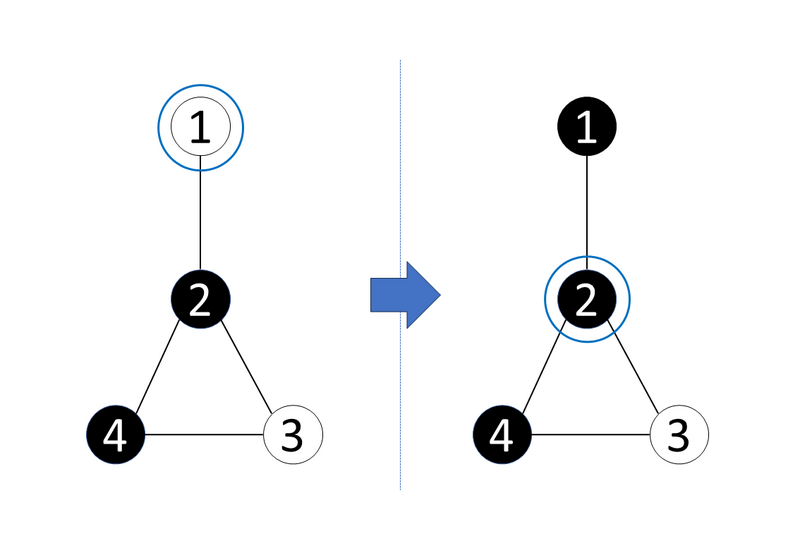
例えば、頂点 1 から出発することを考えます。 最初の動作では、頂点 2 に移動し、移動元である頂点 1 の色を白から黒に変化させます。この際のグラフの変化は下の図の通りです(丸で囲った頂点が今いる頂点を表します)。
その後、頂点 3, 4, 2 へと順に移動すると、この時点で頂点 1,2,3,4 の色は順に黒、白、黒、白となっています。 したがって、次の動作で頂点 1 に移動することができ、出発点に戻ってくることができました。
入力例 2
5 6 1 2 2 3 3 4 4 5 1 4 2 5 0 1 0 1 0
出力例 2
No
このグラフでは、どの頂点を出発点に選んでも、条件を満たすような移動を行って出発点に戻ってくることができません。
Score : 500 points
Problem Statement
There is a simple connected undirected graph with N vertices numbered from 1 to N. This graph has M edges, and the i-th edge connects two vertices a_i and b_i.
Each vertex has a color, either white or black, and the initial state is given by c_i. c_i is either 0 or 1, where c_i=0 means that vertex i is initially white, and c_i=1 means that vertex i is initially black.
On this graph, you can choose any vertex as your starting point and repeat the following operation as many times as you like.
- Move to a vertex of a different color connected by an edge from the current vertex. Immediately after moving, reverse the color of the vertex you moved from (change to black if it was white, and vice versa).
Is it possible to return to the starting point after performing the operation at least once?
Constraints
- 2 \leq N \leq 2 \times 10^5
- N-1 \leq M \leq \mathrm{min} \lbrace 2 \times 10^5,N(N-1)/2 \rbrace
- 1 \leq a_i, b_i \leq N (1 \leq i \leq M)
- c_i=0 or c_i=1 (1 \leq i \leq N)
- The given graph is simple and connected.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M a_1 b_1 a_2 b_2 \vdots a_M b_M c_1 c_2 \ldots c_N
Output
If it is possible to return to the starting point after performing the operation at least once, print Yes; otherwise, print No.
Sample Input 1
4 4 1 2 2 3 3 4 4 2 0 1 0 1
Sample Output 1
Yes
For example, consider starting from vertex 1. In the first operation, move to vertex 2 and change the color of the vertex 1 from white to black. This change in the graph is shown in the figure below (the vertex circled is the current vertex).
Then, if you move to vertices 3, 4, and 2 in order, the colors of vertices 1,2,3,4 will then be black, white, black, and white, respectively. Therefore, you can move to vertex 1 in the next operation, returning to the starting point.

Sample Input 2
5 6 1 2 2 3 3 4 4 5 1 4 2 5 0 1 0 1 0
Sample Output 2
No
In this graph, no matter which vertex you choose as the starting point, you cannot return to the starting point by making moves that satisfy the conditions.
Time Limit: 2 sec / Memory Limit: 1024 MB
配点 : 500 点
問題文
両面に数が書かれた N 枚のカードがあり、i 枚目のカードには片方の面に赤い数字で A_i が、もう片方の面には青い数字で B_i が書かれています。初め、全てのカードは赤い数字が書かれた面を表にして置かれており、Alice と Bob は次のような手順を繰り返すゲームをします。
- まず、Alice が残っているカードの中から 1 枚を選び、裏返す。次に、Bob が残っているカードの中から 1 枚を取り除く。このとき、取り除いたカードの表側の面に書かれていた数の分だけ Bob は得点を得る。
残っているカードが 0 枚になった時、ゲームを終了します。
Alice はゲーム終了時の Bob の得点を最小にしようとし、Bob はこれを最大にしようとします。両者が最善の手順を取ったとき、ゲーム終了時の Bob の得点は何点でしょうか。
制約
- 1\leq N\leq 2\times 10^5
- 1\leq A_i, B_i\leq 10^9 (1\leq i \leq N)
- 入力される値はすべて整数である
入力
入力は以下の形式で標準入力から与えられる。
N A_1 B_1 A_2 B_2 \vdots A_N B_N
出力
答えを整数で出力せよ。
入力例 1
3 6 4 2 1 5 3
出力例 1
12
初めの状態では、表側の面に書かれた数はそれぞれ 6,2,5 です。ここから、例えば次のような進行が考えられます。
- Alice は 1 枚目のカードを裏返す。このとき、表側の面に書かれた数は 4,2,5 となる。Bob は 3 枚目のカードを取り除き、5 点を得る。
- Alice は 2 枚目のカードを裏返す。このとき、表側の面に書かれた数は 4,1 となる。Bob は 2 枚目のカードを取り除き、1 点を得る。
- Alice は最後に残った 1 枚目のカードを裏返す。このとき、表側の面に書かれた数は 6 となる。Bob はこれを取り除き、6 点を得る。
この場合、Bob が最終的に得る得点は 12 点です。実は、この進行は双方の最善手の一例であり、答えは 12 となります。
入力例 2
5 166971716 552987438 219878198 619875818 918378176 518975015 610749017 285601372 701849287 307601390
出力例 2
3078692091
Score : 500 points
Problem Statement
There are N cards, each with a number written on both sides. On the i-th card, the number A_i is written in red on one side, and the number B_i is written in blue on the other side. Initially, all cards are placed with the red number side facing up. Alice and Bob play a game in which they repeat the following steps.
- First, Alice chooses one of the remaining cards and flips it over. Next, Bob removes one of the remaining cards. Then, Bob scores points equal to the number written on the face-up side of the removed card.
The game ends when there are no cards left.
Alice tries to minimize Bob's score at the end of the game, and Bob tries to maximize it. What is Bob's score at the end of the game when both players take optimal steps?
Constraints
- 1\leq N\leq 2\times 10^5
- 1\leq A_i, B_i\leq 10^9 (1\leq i \leq N)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 B_1 A_2 B_2 \vdots A_N B_N
Output
Print the answer as an integer.
Sample Input 1
3 6 4 2 1 5 3
Sample Output 1
12
In the initial state, the numbers written on the face-up sides are 6,2,5. One possible progression from here is as follows.
- Alice flips the first card. Then, the numbers written on the face-up sides are 4,2,5. Bob removes the third card and scores 5 points.
- Alice flips the second card. Then, the numbers written on the face-up sides are 4,1. Bob removes the second card and scores 1 point.
- Alice flips the first card, the final one remaining. Then, the number written on the face-up side is 6. Bob removes it and scores 6 points.
In this case, Bob's final score is 12 points. In fact, this progression is an example of optimal sequences of moves for both players; the answer is 12.
Sample Input 2
5 166971716 552987438 219878198 619875818 918378176 518975015 610749017 285601372 701849287 307601390
Sample Output 2
3078692091
Time Limit: 2 sec / Memory Limit: 1024 MB
配点 : 600 点
問題文
長さ 2N で + , - が N 個ずつからなる文字列 s に対して次の問題を考え、その答えを p(s) と書くことにします。
数直線上の x=1,2,3,\ldots , 2N の位置に 2N 個のボールが並んでおり、そのうち N 個は +1 の、残りの N 個は -1 の電荷を持ちます。ボールの持つ電荷の並び方は s によって表され、s の i 文字目が
+であれば x=i には +1 の電荷を持つボールが、-であれば x=i には -1 の電荷を持つボールが配置されていることを表します。それぞれのボールは、次の規則にしたがって、一斉に運動を始めます。ただし、数直線上でより小さい数が位置する方向を左、より大きい数が位置する方向を右と呼びます。
- 各ボールに対して、各時点で F を次の式で定める
F=\lbrace (自身より真に左に存在するボールの電荷の総和) - (自身より真に右に存在するボールの電荷の総和) \rbrace \times (自身の電荷)- 各ボールは各時点で、F が正であれば右に、負であれば左に、毎秒 1 の速さで動く
- 同時に同じ座標に電荷 +1 のボールと電荷 -1 のボールが存在した場合、両者は打ち消しあって消滅する
このとき、それぞれのボールが運動を始めてから消滅するまでに移動した距離(消滅した座標と初めの座標の差の絶対値)の総和はいくつでしょうか。
長さ 2N で、+ , - , ? からなる文字列 T が与えられます。T の ? を + または - に置換することで得られる、 + , - が N 個ずつからなる文字列 s 全てについての p(s) の総和を 998244353 で割った余りを求めてください。
なお、与えられた制約と運動の規則の下で、有限の時間内に全てのボールが消滅すること、ボールが消滅しない限り各ボールの F の値が 0 にならないこと、3 つ以上のボールが同時に同じ座標に位置する瞬間が無いこと、および p(s) が整数になることが示せます。
制約
- 1\leq N\leq 3000
- N は整数である
- |T|=2N
- T の各文字は
+,-,?のいずれかであり、+と-はそれぞれ N 個以下である
入力
入力は以下の形式で標準入力から与えられる。
N T
出力
答えを 998244353 で割った余りを整数で出力せよ。
入力例 1
2 +??-
出力例 1
6
T から得られる文字列 s として、 ++-- と +-+- が考えられます。
++-- について、運動を開始した時点では各ボールの左右の電荷の総和、および F の値は次のようになります。

したがって、x=1,2 のボールは右に、x=3,4 のボールは左に動き始めます。
この場合、各ボールはその後運動の向きを変えることなく、 0.5 秒後に x=2,3 にあったボールが x=2.5 で、1.5 秒後に x=1,4 にあったボールが x=2.5 でそれぞれ消滅します。
この間に、x=2,3 にあったボールは 0.5 ずつ、x=1,4 にあったボールは 1.5 ずつの距離を移動しているため、p( ++-- )=4 です。
同様に観察すると p( +-+- )=2 であることが分かるため、求める p(s) の総和は 6 となります。
入力例 2
17 ??????????????????????????????????
出力例 2
285212526
p(s) の総和を 998244353 で割った余りを出力してください。
Score : 600 points
Problem Statement
Consider the following problem for a string s of length 2N formed by N + and N -, and let p(s) denote the answer.
There are 2N balls lined up at positions x=1,2,3,\ldots , 2N on a number line, of which N have a charge of +1 and the remaining N have a charge of -1. The arrangement of the charges of the balls is represented by s. If the i-th character of s is
+, a ball with a charge of +1 is placed at x=i; if it is-, a ball with a charge of -1 is placed at x=i.Each ball starts motion simultaneously according to the following rules. Here, we call the direction where smaller numbers are located on the number line "left", and the direction where larger numbers are located "right".
- For each ball, define F at each moment by the following formula:
F=\lbrace (the sum of the charges of the balls strictly to the left of itself) - (the sum of the charges of the balls strictly to the right of itself) \rbrace \times (the charge of itself).- At each moment, each ball moves to the right if F is positive, and to the left if F is negative, at a speed of 1 per second.
- If a ball with a charge of +1 and a ball with a charge of -1 exist at the same coordinate simultaneously, they cancel out each other and disappear.
Then, what is the sum of the distances moved by the balls after they start motion and before they disappear (the distance moved by a ball is the absolute difference between the coordinates where it starts and where it disappears)?
You are given a string T of length 2N consisting of +, -, and ?. Find the sum of p(s) over all strings s formed by N + and N - that can be obtained by replacing each ? in T with + or -, modulo 998244353.
Under the given constraints and the rules of motion, it can be shown that all balls disappear in finite time, that the value of F for each ball does not become 0 until that ball disappears, that there is no moment when three or more balls are at the same coordinate simultaneously, and that p(s) is an integer.
Constraints
- 1\leq N\leq 3000
- N is an integer.
- |T|=2N
- Each character of T is either
+,-, or?, and there are at most N+and at most N-.
Input
The input is given from Standard Input in the following format:
N T
Output
Print the answer modulo 998244353, as an integer.
Sample Input 1
2 +??-
Sample Output 1
6
The strings s that can be obtained from T are ++-- and +-+-.
For ++--, the sum of the charges of the balls to the left and right of each ball, and the value of F at the start of the motion are as follows:

Thus, the balls at x=1,2 start moving to the right, and the balls at x=3,4 start moving to the left.
Then, each ball continues to move in the same direction without changing its direction of motion, and the balls that started at x=2,3 disappear at x=2.5 after 0.5 seconds, and the balls that started at x=1,4 disappear at x=2.5 after 1.5 seconds.
During these times, the balls that started at x=2,3 move a distance of 0.5 each, and the balls that started at x=1,4 move a distance of 1.5 each, so p( ++-- )=4.
Similarly, it can be seen that p( +-+- )=2, so the sought sum of p(s) is 6.
Sample Input 2
17 ??????????????????????????????????
Sample Output 2
285212526
Be sure to print the sum of p(s) modulo 998244353.
Time Limit: 2 sec / Memory Limit: 1024 MB
配点 : 700 点
問題文
N 項からなる数列があり、これから Q 個のクエリが与えられます。 i 番目のクエリでは区間 [L_i, R_i] に対するクエリが与えられます(区間 [a,b] は a 以上 b 以下の整数からなる集合です)。
あなたは、この問題に、下記の条件を満たす二分木を用いて答えます。ただし、以下の記述で i,j,k は整数を表します。
- 各頂点は区間を持つ
- 根となる頂点は区間 [1, N] を持つ
- 区間 [i, i] を持つ頂点は葉である。また、葉が持つ区間は [i,i] と表される
- 葉でない頂点にはちょうど 2 個の子が存在する。また、葉でない頂点が持つ区間を [i,j] とすると、この頂点の子が持つ区間は [i,k] と [k+1,j] である(i\leq k<j)
この二分木では区間 [L,R] に対するクエリが与えられると、以下の規則で再帰的に探索が行われます。
- はじめに、根が調査される
- ある頂点が調査されたとき、この頂点の持つ区間が [L, R] に含まれるならば、子孫は調査しない
- ある頂点が調査されたとき、この頂点の持つ区間と [L, R] が共通部分を持たないならば、子孫は調査しない
- ある頂点が調査されたとき、2,3 のどちらにも当てはまらなければ、子である頂点 2 つを調査する(なお、葉である頂点は必ず 2,3 のどちらかに当てはまることが示せる)
Q 個のクエリに答える時、調査された頂点の深さ(根からの距離)の最大値を d 、深さ d の頂点が調査された回数の総和を c とします。ただし、一つのクエリで複数個の深さ d の頂点が調査された場合、および同じ頂点が複数のクエリで調査された場合にはそれぞれ複数回数えます。
あなたは二分木を適切に設計し、d を最小にしたのち、その範囲内で c を最小にしたいと考えています。このときの d および c の値はいくつでしょうか。
制約
- 2\leq N \leq 4000
- 1\leq Q \leq 10^5
- 1\leq L_i \leq R_i \leq N (1\leq i \leq Q)
- 入力される値はすべて整数である
入力
入力は以下の形式で標準入力から与えられる。
N Q L_1 R_1 L_2 R_2 \vdots L_Q R_Q
出力
題意の d, c をこの順に空白区切りで整数で出力せよ。
入力例 1
6 4 2 3 3 4 2 4 3 3
出力例 1
3 4
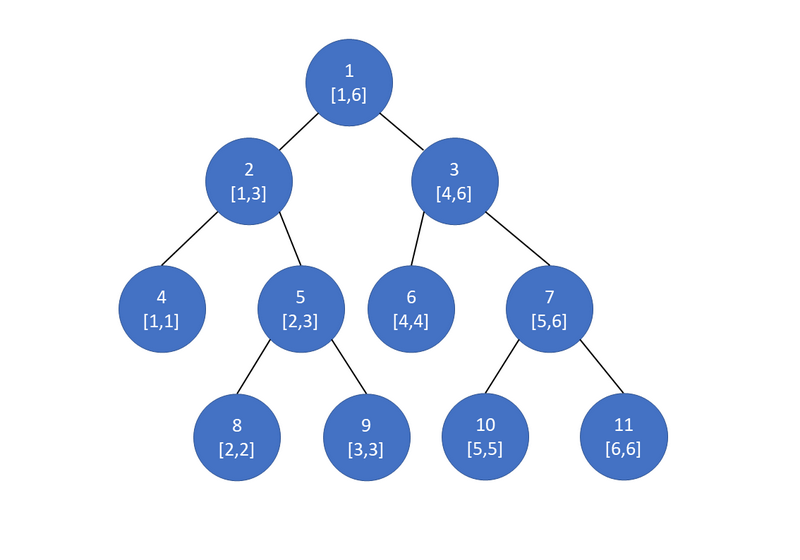
区間 [1,6] に対して、区間 [2,3],[3,4],[2,4],[3,3] に対するクエリが与えられています。このとき、下の図のような二分木を用いると、
- 1 つめのクエリについては、頂点 1,2,3,4,5 が調査され、この中で最大の深さは頂点 4,5 の 2
- 2 つめのクエリについては、頂点 1,2,3,4,5,6,7,8,9 が調査され、この中で最大の深さは頂点 8,9 の 3
- 3 つめのクエリについては、頂点 1,2,3,4,5,6,7 が調査され、この中で最大の深さは頂点 4,5,6,7 の 2
- 4 つめのクエリについては、頂点 1,2,3,4,5,8,9 が調査され、この中で最大の深さは頂点 8,9 の 3
となります。したがって、この場合は d=3 であり、深さ 3 の頂点が調査された回数は 2 つめのクエリの際の頂点 8,9 、 4 つめのクエリの際の頂点 8,9 で計 4 回であるため、c=4 となります。実はこれは最適な方法の一例です。
(図の上段が頂点の番号、下段が各頂点が持つ区間です。)
入力例 2
12 6 1 10 2 7 3 6 4 9 5 8 11 12
出力例 2
4 4
Score : 700 points
Problem Statement
There is a sequence of N terms, and Q queries will be given on this sequence. The i-th query is for the interval [L_i, R_i] (the interval [a,b] is a set of integers between a and b, inclusive).
You will answer this problem using a binary tree that satisfies the following conditions. Here, i,j,k represent integers.
- Each node has an interval.
- The root node has the interval [1, N].
- The node with the interval [i, i] is a leaf. Also, the interval of a leaf can be represented as [i,i].
- Each non-leaf node has exactly two children. Also, if the interval of a non-leaf node is [i,j], the intervals of the children of this node are [i,k] and [k+1,j] (i\leq k<j).
In this binary tree, when a query for the interval [L,R] is given, a search is performed recursively according to the following rules.
- Initially, the root is investigated.
- When a node is investigated, if the interval of this node is included in [L, R], its descendants are not investigated.
- When a node is investigated, if the interval of this node have no intersection with [L,R], its descendants are not investigated.
- When a node is investigated, if neither 2. nor 3. applies, the two child nodes are investigated. (It can be shown that either 2. or 3. always applies to a leaf node.)
When answering Q queries, let d be the maximum depth (distance from the root) of the investigated nodes, and c be the total number of times nodes of depth d are investigated. Here, if multiple nodes of depth d are investigated in a single query, or if the same node is investigated in multiple queries, all those investigations count separately.
You want to design the binary tree to minimize d, and then to minimize c while minimizing d. What are the values of d and c then?
Constraints
- 2\leq N \leq 4000
- 1\leq Q \leq 10^5
- 1\leq L_i \leq R_i \leq N (1\leq i \leq Q)
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N Q L_1 R_1 L_2 R_2 \vdots L_Q R_Q
Output
Print the integers d and c in question, in this order, separated by a space.
Sample Input 1
6 4 2 3 3 4 2 4 3 3
Sample Output 1
3 4
We have an interval [1,6], and queries for the intervals [2,3],[3,4],[2,4],[3,3]. Here, if you use the binary tree shown in the figure below,
- for the first query, nodes 1,2,3,4,5 are investigated, and the maximum depth among these is 2 for nodes 4,5;
- for the second query, nodes 1,2,3,4,5,6,7,8,9 are investigated, and the maximum depth among these is 3 for nodes 8,9;
- for the third query, nodes 1,2,3,4,5,6,7 are investigated, and the maximum depth among these is 2 for nodes 4,5,6,7;
- for the fourth query, nodes 1,2,3,4,5,8,9 are investigated, and the maximum depth among these is 3 for nodes 8,9.
Therefore, in this case, d=3, and nodes of depth 3 were investigated four times ー nodes 8,9 in the second query and nodes 8,9 in the fourth query ー so c=4. In fact, this is an optimal method.
(In the figure, the upper row shows the node number, and the lower row shows the interval of each node.)

Sample Input 2
12 6 1 10 2 7 3 6 4 9 5 8 11 12
Sample Output 2
4 4
Time Limit: 2 sec / Memory Limit: 1024 MB
配点 : 900 点
問題文
頂点に 1 から N までの番号がついており、頂点 1 を根とする N 頂点の根付き木が与えられます。 この木の頂点 i の親は頂点 p_i です(2\leq i\leq N)。
Alice と Bob は、この木を使って、次のようなゲームを行います。
- Alice が先手、Bob が後手で、表裏を白と黒に塗り分けた石を使い、交互に 1 つずつ木の頂点に石を置いていく。この際、Alice は白い面を上に、Bob は黒い面を上にして置く。
- 各手番で石を置いてよいのは、その頂点自身には石が置かれておらず、子孫である頂点には全て石が置かれている頂点のみである。
- 石を置くとき、置いた頂点の子孫にある石を全て裏返す(置いた石自体は裏返さない)。
全ての頂点に石が置かれるとゲーム終了となり、この時点で白い面が上になっている石の数を Alice の得点とします。
Alice はできるだけ大きな得点を得ようとし、Bob は Alice の得点をできるだけ小さくしようとします。両者が最善の手順を取ったとき、Alice の得点はいくらでしょうか。
制約
- 2 \leq N \leq 2 \times 10^5
- 1 \leq p_i < i (2\leq i \leq N)
- 入力される値はすべて整数である
- 与えられるグラフは木である
入力
入力は以下の形式で標準入力から与えられる。
N p_2 p_3 \ldots p_N
出力
答えを整数で出力せよ。
入力例 1
4 1 1 2
出力例 1
2
与えられた木では、初めに石を置くことのできる頂点は 3,4 のみです。ここから、例えば次のような進行が考えられます。
- Alice が頂点 4 に白い面を上にして石を置く。この操作の後、頂点 2 は子孫に全て石が置かれたので、石が置けるようになる。
- Bob が頂点 2 に黒い面を上にして石を置き、頂点 4 にある石を裏返して黒い面を上にする。
- Alice が頂点 3 に白い面を上にして石を置く。
- Bob が頂点 1 に黒い面を上にして石を置き、頂点 2,3,4 にある石を全て裏返す。
この場合、ゲーム終了時に頂点 1,2,3,4 にある石はそれぞれ黒、白、黒、白が上になっています。実は、この進行は双方の最善手の一例であり、答えは 2 となります。
入力例 2
7 1 1 2 4 4 4
出力例 2
5
Score : 900 points
Problem Statement
You are given a rooted tree with N vertices numbered from 1 to N, rooted at vertex 1. The parent of vertex i is vertex p_i (2\leq i\leq N).
Alice and Bob play a game using this tree as follows.
- Alice goes first, and Bob goes second. They take turns placing a stone, with a white side and a black side, on a vertex of the tree. Alice places the stone with the white side up, and Bob places the stone with the black side up.
- In each turn, a stone can only be placed on a vertex that does not have a stone on itself while all its descendants already have stones on them.
- When placing a stone on a vertex, all the stones on the descendants of that vertex are flipped over (the placed stone itself is not flipped).
The game ends when all vertices have stones. Alice's score is the number of stones with the white side up at this point.
Alice tries to maximize her score, and Bob tries to minimize Alice's score. If both play optimally, what will be Alice's score?
Constraints
- 2 \leq N \leq 2 \times 10^5
- 1 \leq p_i < i (2\leq i \leq N)
- All input values are integers.
- The given graph is a tree.
Input
The input is given from Standard Input in the following format:
N p_2 p_3 \ldots p_N
Output
Print the answer as an integer.
Sample Input 1
4 1 1 2
Sample Output 1
2
In the given tree, the only vertices where a stone can be placed initially are 3 and 4. One possible progression from here is as follows.
- Alice places a stone with the white side up on vertex 4. After this operation, all descendants of vertex 2 have stones, so it is now possible to place a stone on vertex 2.
- Bob places a stone with the black side up on vertex 2 and flips the stone on vertex 4 to have the black side up.
- Alice places a stone with the white side up on vertex 3.
- Bob places a stone with the black side up on vertex 1 and flips all the stones on vertices 2, 3, and 4.
In this case, at the end of the game, the stones on vertices 1, 2, 3, and 4 have black, white, black, and white sides up, respectively. In fact, this progression is an example of optimal sequences of moves for both players; the answer is 2.
Sample Input 2
7 1 1 2 4 4 4
Sample Output 2
5