 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 900 点
問題文
すぬけくんは (0,1,2, ...,N-1) を並び替えて得られるような数列 p を持っています。 p の (0-indexedでの) i 番目の数は p_i です。
すぬけくんは 1,2,...,N-1 の番号がついた N-1 種類の操作を自由な順番で何度でも行うことができます。 k 番の操作を行うと以下のソースコードで表されるような処理が実行されます。
for(int i=k;i<N;i++)
swap(p[i],p[i-k]);
すぬけくんは操作を 0 回以上 10^{5} 回以下行って p を昇順に並び替えたいです。そのような操作手順の一例を示してください。 なお、この問題の制約下で、そのような操作手順が必ず存在することが証明できます。
制約
- 2 \leq N \leq 200
- 0 \leq p_i \leq N-1
- p は (0,1,2,...,N-1) を並び替えて得られる
部分点
- 300 点分のデータセットでは N \leq 7 が成立する
- 別の 400 点分のデータセットでは N \leq 30 が成立する
入力
入力は以下の形式で標準入力から与えられる。
N
p_0 p_1 ... p_{N-1}
出力
操作回数(これを m とする)を 1 行目に出力せよ。 続く m 行のうち i 行目には i 番目に実行する操作の番号を出力せよ。 m が 10^5 以下であり、m 回の操作後に p が昇順となっていれば正解となる。
入力例 1
5 4 2 0 1 3
出力例 1
4 2 3 1 2
- 以下の図に各操作による p の変化を示します。
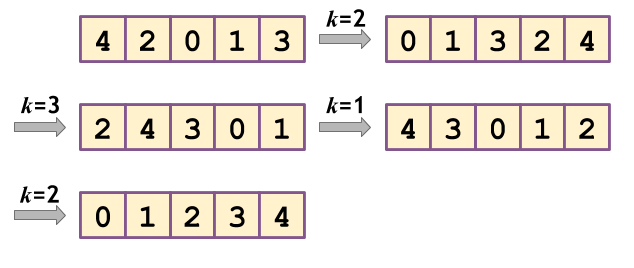
入力例 2
9 1 0 4 3 5 6 2 8 7
出力例 2
11 3 6 1 3 5 2 4 7 8 6 3
Score : 900 points
Problem Statement
Snuke has a sequence p, which is a permutation of (0,1,2, ...,N-1). The i-th element (0-indexed) in p is p_i.
He can perform N-1 kinds of operations labeled 1,2,...,N-1 any number of times in any order. When the operation labeled k is executed, the procedure represented by the following code will be performed:
for(int i=k;i<N;i++)
swap(p[i],p[i-k]);
He would like to sort p in increasing order using between 0 and 10^{5} operations (inclusive). Show one such sequence of operations. It can be proved that there always exists such a sequence of operations under the constraints in this problem.
Constraints
- 2 \leq N \leq 200
- 0 \leq p_i \leq N-1
- p is a permutation of (0,1,2,...,N-1).
Partial Scores
- In the test set worth 300 points, N \leq 7.
- In the test set worth another 400 points, N \leq 30.
Input
Input is given from Standard Input in the following format:
N
p_0 p_1 ... p_{N-1}
Output
Let m be the number of operations in your solution. In the first line, print m. In the i-th of the following m lines, print the label of the i-th executed operation. The solution will be accepted if m is at most 10^5 and p is in increasing order after the execution of the m operations.
Sample Input 1
5 4 2 0 1 3
Sample Output 1
4 2 3 1 2
- Each operation changes p as shown below:

Sample Input 2
9 1 0 4 3 5 6 2 8 7
Sample Output 2
11 3 6 1 3 5 2 4 7 8 6 3