 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 800 点
問題文
すぬけフェスティバル2017が 1,2, ...,N の番号がついた N 頂点の木で開催されます。 この木の i 番目の辺は頂点 a_i と b_i をつなぐ楽しさ c_i の辺です。
すぬけくんと N-1 匹の黒猫がスタッフです。 すぬけくんはある頂点に本部を設置し、それ以外の N-1 個の頂点にそれぞれ黒猫を 1 匹派遣しようと考えています。
全ての頂点について、その頂点に本部を設置したときの 良さ を計算してください。 頂点 i に本部を置いたときの良さは以下のようにして計算されます。
- X=0 とする
- 1 以上 N 以下の整数 j (ただし i を除く)について、以下の処理を行う
- 頂点 i から頂点 j への経路の途中にある辺のうち、最も楽しさが小さいような辺の楽しさ c を X に加算する
- 最終的な X の値が良さである
制約
- 1 \leq N \leq 10^{5}
- 1 \leq a_i,b_i \leq N
- 1 \leq c_i \leq 10^{9}
- 与えられるグラフは木
- 与えられる入力は全て整数
部分点
- 200 点分のデータセットでは N \leq 1000 が成立する
- 200 点分のデータセットでは c_i \leq 2 が成立する
入力
入力は以下の形式で標準入力から与えられる。
N
a_1 b_1 c_1
:
a_{N-1} b_{N-1} c_{N-1}
出力
N 行に答えを出力せよ。 i 行目には頂点 i に本部を設置したときの良さを出力せよ。
入力例 1
3 1 2 10 2 3 20
出力例 1
20 30 30
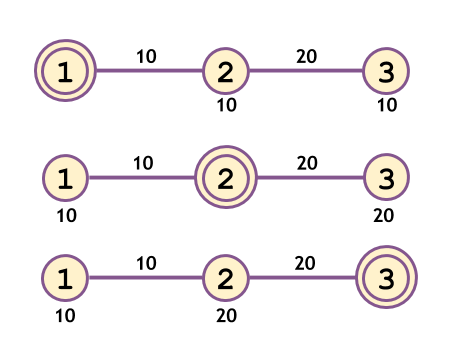
- 以下の図に頂点 1,2,3 に本部を設置した場合をそれぞれ示します
- 辺の上に書かれた数はその辺の楽しさを、頂点の下に書かれた数は本部からその頂点への経路の途中にある辺のうち、最も楽しさが小さいような辺の楽しさを示します
入力例 2
15 6 3 2 13 3 1 1 13 2 7 1 2 8 1 1 2 8 2 2 12 2 5 2 2 2 11 2 10 2 2 10 9 1 9 14 2 4 14 1 11 15 2
出力例 2
16 20 15 14 20 15 16 20 15 20 20 20 16 15 20
入力例 3
19 19 14 48 11 19 23 17 14 30 7 11 15 2 19 15 2 18 21 19 10 43 12 11 25 3 11 4 5 19 50 4 11 19 9 12 29 14 13 3 14 6 12 14 15 14 5 1 6 8 18 13 7 16 14
出力例 3
103 237 71 263 370 193 231 207 299 358 295 299 54 368 220 220 319 237 370
Score : 800 points
Problem Statement
Snuke Festival 2017 will be held in a tree with N vertices numbered 1,2, ...,N. The i-th edge connects Vertex a_i and b_i, and has joyfulness c_i.
The staff is Snuke and N-1 black cats. Snuke will set up the headquarters in some vertex, and from there he will deploy a cat to each of the other N-1 vertices.
For each vertex, calculate the niceness when the headquarters are set up in that vertex. The niceness when the headquarters are set up in Vertex i is calculated as follows:
- Let X=0.
- For each integer j between 1 and N (inclusive) except i, do the following:
- Add c to X, where c is the smallest joyfulness of an edge on the path from Vertex i to Vertex j.
- The niceness is the final value of X.
Constraints
- 1 \leq N \leq 10^{5}
- 1 \leq a_i,b_i \leq N
- 1 \leq c_i \leq 10^{9}
- The given graph is a tree.
- All input values are integers.
Partial Scores
- In the test set worth 200 points, N \leq 1000.
- In the test set worth 200 points, c_i \leq 2.
Input
Input is given from Standard Input in the following format:
N
a_1 b_1 c_1
:
a_{N-1} b_{N-1} c_{N-1}
Output
Print N lines. The i-th line must contain the niceness when the headquarters are set up in Vertex i.
Sample Input 1
3 1 2 10 2 3 20
Sample Output 1
20 30 30
- The figure below shows the case when headquarters are set up in each of the vertices 1, 2 and 3.
- The number on top of an edge denotes the joyfulness of the edge, and the number below an vertex denotes the smallest joyfulness of an edge on the path from the headquarters to that vertex.

Sample Input 2
15 6 3 2 13 3 1 1 13 2 7 1 2 8 1 1 2 8 2 2 12 2 5 2 2 2 11 2 10 2 2 10 9 1 9 14 2 4 14 1 11 15 2
Sample Output 2
16 20 15 14 20 15 16 20 15 20 20 20 16 15 20
Sample Input 3
19 19 14 48 11 19 23 17 14 30 7 11 15 2 19 15 2 18 21 19 10 43 12 11 25 3 11 4 5 19 50 4 11 19 9 12 29 14 13 3 14 6 12 14 15 14 5 1 6 8 18 13 7 16 14
Sample Output 3
103 237 71 263 370 193 231 207 299 358 295 299 54 368 220 220 319 237 370