 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 1000 点
問題文
すぬけくんは以下のような問題を考えました。
長さ N の数列 d が与えられます。 以下の条件を満たす頂点に 1,2,...,N のラベルがついた N 頂点の無向グラフの数を modulo 10^{9} + 7 で求めてください。
- グラフは単純かつ連結
- 頂点 i の次数は d_i
2 \leq N, 1 \leq d_i \leq N-1, {\rm Σ} d_i = 2(N-1) を満たす場合 には、この問題の答えは \frac{(N-2)!}{(d_{1} -1)!(d_{2} - 1)! ... (d_{N}-1)!} で表せることが証明できます。
すぬけくんは 3 \leq N, 1 \leq d_i \leq N-1, { \rm Σ} d_i = 2N を満たす場合 どうなるかが気になっています。 すぬけくんの代わりにこの問題を解いてください。
制約
- 3 \leq N \leq 300
- 1 \leq d_i \leq N-1
- { \rm Σ} d_i = 2N
部分点
- 200 点分のデータセットでは N \leq 5 が成立する
- 別の 200 点分のデータセットでは N \leq 18 が成立する
- 別の 300 点分のデータセットでは N \leq 50 が成立する
入力
入力は以下の形式で標準入力から与えられる。
N
d_1 d_2 ... d_{N}
出力
答えを出力せよ。
入力例 1
5 1 2 2 3 2
出力例 1
6
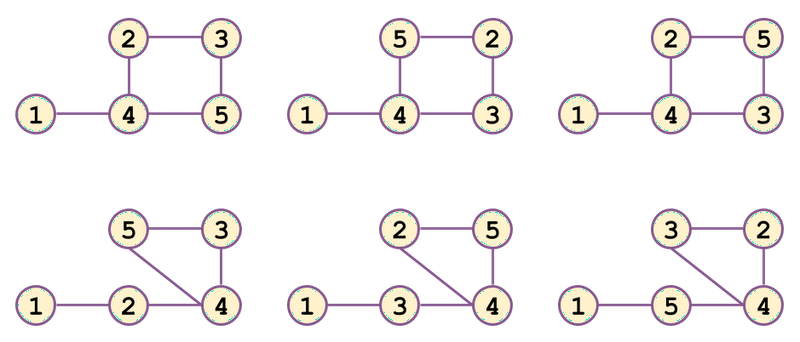
- 以下の図に示されるような 6 通りです
入力例 2
16 2 1 3 1 2 1 4 1 1 2 1 1 3 2 4 3
出力例 2
555275958
- 10^{9} + 7 で割ったあまりを求めてください
Score : 1000 points
Problem Statement
Snuke has come up with the following problem.
You are given a sequence d of length N. Find the number of the undirected graphs with N vertices labeled 1,2,...,N satisfying the following conditions, modulo 10^{9} + 7:
- The graph is simple and connected.
- The degree of Vertex i is d_i.
When 2 \leq N, 1 \leq d_i \leq N-1, {\rm Σ} d_i = 2(N-1), it can be proved that the answer to the problem is \frac{(N-2)!}{(d_{1} -1)!(d_{2} - 1)! ... (d_{N}-1)!}.
Snuke is wondering what the answer is when 3 \leq N, 1 \leq d_i \leq N-1, { \rm Σ} d_i = 2N. Solve the problem under this condition for him.
Constraints
- 3 \leq N \leq 300
- 1 \leq d_i \leq N-1
- { \rm Σ} d_i = 2N
Partial Scores
- In the test set worth 200 points, N \leq 5.
- In the test set worth another 200 points, N \leq 18.
- In the test set worth another 300 points, N \leq 50.
Input
Input is given from Standard Input in the following format:
N
d_1 d_2 ... d_{N}
Output
Print the answer.
Sample Input 1
5 1 2 2 3 2
Sample Output 1
6
- There are six graphs as shown below:

Sample Input 2
16 2 1 3 1 2 1 4 1 1 2 1 1 3 2 4 3
Sample Output 2
555275958
- Be sure to find the answer modulo 10^{9} + 7.