B - 立方体とペンキ
Editorial
 /
/ 
 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
問題文
りんごさんは 1 辺の長さが 1 の立方体を積んで遊んでいます。りんごさんは地面に 1 辺の長さが 1 の正方形を横に並べて N 個描き、左から i 個目の正方形の上に立方体を A_i 個積みました。
りんごさんは立方体の表面にペンキを塗ることにしました。別の立方体や地面と接している面にはペンキを塗りません。しかし、りんごさんはペンキの量が足りるか不安になりました。そこで、K 個の立方体を取り除いてからペンキを塗ることにしました。このとき、いずれの正方形の上にも 1 個以上の立方体がなければなりません。
りんごさんは必要なペンキの量をできるだけ少なくしたいです。ペンキを塗る面積の最小値を求めてください。
入力
入力は以下の形式で標準入力から与えられる。
N K A_1 A_2 ... A_N
- 1 行目には、2 つの整数 N (1 ≦ N ≦ 10^5), K (1 ≦ K ≦ 10^{14}) が空白区切りで与えられる。これは、地面に描いた正方形の個数が N 個、取り除く立方体の個数が K 個であることを表す。
- 2 行目には、各正方形の上に積む立方体の個数を表す N 個の整数が空白区切りで与えられる。このうち i (1 ≦ i ≦ N) 番目の整数 A_i (1 ≦ A_i ≦ 10^9) は、左から i 個目の正方形の上に積む立方体の個数を表す。ただし、いずれの正方形の上にも 1 個以上の立方体を残して K 個の立方体を取り除くことができること、すなわち Σ A_i ≧ N+K が保証される。
出力
ペンキを塗る面積の最小値を 1 行に出力せよ。出力の末尾に改行を入れること。
入力例1
7 6 2 3 2 1 2 3 4
出力例1
35
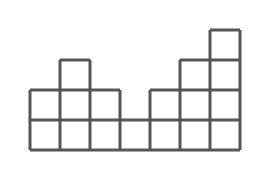
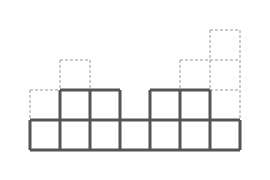
下図は、はじめに積んだ立方体を正面から見たときの様子を表しています。

下図のように 6 個の立方体を取り除くと、ペンキを塗る面積は 35 となります。

入力例2
10 919924177 114777581 900857217 199708389 41623648 586160911 824291566 209849198 803644124 355106148 180322764
出力例2
9307626516