 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
問題文
ドーナツ屋の店員の須藤なつきさんはドーナツの箱詰めの担当です。なつきさんは今、K 個のドーナツを N 個の箱に箱詰めしようとしています。箱 i (1 ≦ i ≦ N) の体積は C_i で、どの箱もドーナツを 1 つ入れることができます。
なつきさんは全ての箱を使いたいと思っています。しかし、ドーナツの個数よりも箱の個数の方が多いため、箱の中に箱を入れ子にすることによって箱を使い切ることにしました。各箱の中には、ドーナツまたは箱のいずれか一方を必ずちょうど 1 個入れることにしました。箱 i には箱 i よりも体積が小さい箱を入れることができます。また、中に入れる箱の中にさらに箱やドーナツが入っていた場合でもその箱は 1 個として数えます。箱 i の中に箱 j を入れた場合には、箱 i と箱 j の間に C_{i} - C_{j} の量の緩衝材を入れなければなりません。このとき、必要な緩衝材の量の和の最小値を求めてください。
また、なつきさんはとても不器用なので箱詰めの途中で箱を潰してしまうことがあります。なつきさんが箱を潰すごとに、その時点で残っている箱を全て使って箱詰めをするときに必要な緩衝材の量の和の最小値を求めてください。なつきさんは合計 Q 個の箱を潰し、i 個目に潰した箱は箱 D_i です。
入力
入力は以下の形式で標準入力から与えられる。
N K C_1 C_2 ... C_N Q D_1 D_2 : D_Q
- 1 行目には、2 つの整数 N (1 ≦ N ≦ 200,000), K (1 ≦ K ≦ N) が空白区切りで与えられる。これは、はじめに箱が N 個とドーナツが K 個あるということを表す。
- 2 行目には、箱の体積を表す N 個の整数が空白区切りで与えられる。このうち i 番目の整数 C_i (1 ≦ C_i ≦ 200,000) は、箱 i の体積を表す。ただし、p \neq q のとき C_p \neq C_q であることが保証される。
- 3 行目には、なつきさんが潰した箱の個数を表す整数 Q (0 ≦ Q ≦ N-K) が与えられる。
- 4 行目からの Q 行には、なつきさんが潰した箱の情報が与えられる。このうち i 行目には、整数 D_i (1 ≦ D_i ≦ N) が与えられる。これは、なつきさんが i 個目に潰した箱が箱 D_i であることを表す。ただし、p \neq q のとき D_p \neq D_q であることが保証される。
部分点
この問題には部分点が設定されている。
- Q = 0 かつ K = 2 を満たすデータセット 1 に正解した場合は、15 点が与えられる。
- Q = 0 を満たすデータセット 2 に正解した場合は、上記とは別に 25 点が与えられる。
- K = 2 を満たすデータセット 3 に正解した場合は、上記とは別に 30 点が与えられる。
出力
出力は Q+1 行からなる。1 行目には、N 個の箱を全て使って箱詰めをするときに必要な緩衝材の量の和の最小値を出力し、2 行目から Q+1 行目までのうち i (1 ≦ i ≦ Q) 行目には、i 個目までの箱を潰した時点で残っている箱を全て使って箱詰めをするときに必要な緩衝材の量の和の最小値を出力せよ。出力の末尾にも改行を入れること。
入力例1
5 4 1 9 3 7 4 0
出力例1
1
このケースでは図のような箱詰めの仕方をすると必要な緩衝材の量が 1 となり最小となります。青い部分は緩衝材を入れる部分を表しています。
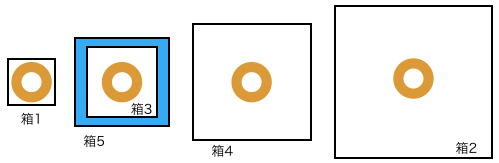
また、このケースではなつきさんは箱を 1 個も潰しません。
入力例2
4 2 6 5 10 2 2 3 1
出力例2
4 1 0
このケースでは図のような箱詰めの仕方をすると良いです。青い部分は緩衝材を入れる部分を表しています。
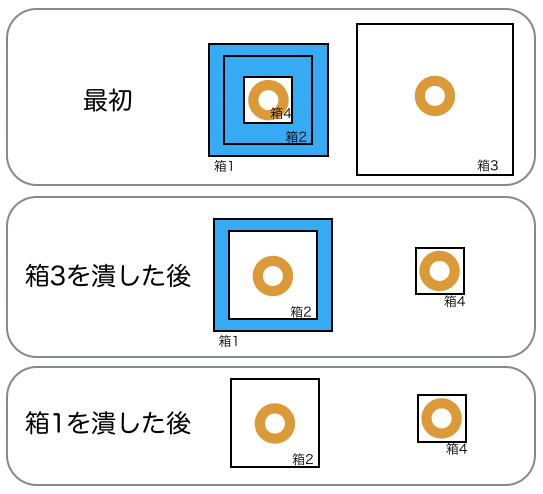
入力例3
7 3 2 12 3 13 7 17 1 4 4 3 1 6
出力例3
7 6 6 5 0