Time Limit: 2 sec / Memory Limit: 128 MB
Problem Statement
A君は山手線に乗って目的地にたどり着きたい.
A君は電車に乗ってから $a$ 分起きて $b$ 分寝ることを繰り返す. 目的地までは乗車後 $c$ 分であり,このとき起きていれば下車できるが,逆に寝ている途中であれば乗り過ごしてしまう.また,A君は乗り過ごしてもずっと同じ電車に乗り続け,電車は山手線を一周するのに60分かかる.したがって,A君は目的地に $60t+c$ ( $t$ は非負整数) 分後に着くことになる.
何分後にA君は目的地に到着できるか. 到着不可能なときは-1を出力せよ.
ただし,目的地に到着した時が寝ている時間と起きている時間の境目だった場合は降りることができるものとする.
Input
入力は以下の形式で1行で与えられる.
$a$ $b$ $c$
入力は3つの整数 $a, b, c$ からなる.
$a$ は起きている時間,$b$ は寝ている時間,$c$ は乗車してから目的地までにかかる時間である.
また,$a, b, c$ の単位は分である.
Constraints
$0 < a, b, c < 60$
Output
A君が目的地に到着できる場合はA君の目的地到着までにかかる時間を出力せよ.それ以外の場合は-1を出力せよ.
Sample Input 1
10 10 5
Output for the Sample Input 1
5
- 寝る前に目的地にたどり着く.
Sample Input 2
50 40 51
Output for the Sample Input 2
111
- 一回乗り過ごしてしまう.
Sample Input 3
20 20 20
Output for the Sample Input 3
20
- もうちょっとで寝るところだったがなんとか目的地で起きていられた.
Sample Input 4
30 30 40
Output for the Sample Input 4
-1
- 一周の前半では起きているが後半で寝ているということを繰り返す.
- このため目的地にはたどり着けない.
Time Limit: 2 sec / Memory Limit: 128 MB
Problem Statement
AさんとB君は,$N \times M$ の長方形のマス目状の地域に住んでいる.各マス目は道か壁か家のどれかである. この地域は,道が複雑で入り組んでいるので痴漢被害がよく起こることで有名であるため,この地域と外部との境界は全て壁で囲まれており,隔離されている.
B君はなんとなく気が向いたので,Aさんの家を眺めに行くことにした.しかし,不幸なことにB君は明らかに怪しい顔をしているので,Aさんの家に行く途中に少しでも痴漢の疑いがあるような行動を取ったらすぐに捕まってしまうだろう.特に,右手を壁から離して歩くことは絶対にやってはならない.B君は,一瞬たりとも右手を離すことなく,Aさんの家に辿り着くことが出来るだろうか?
B君はつねに上下左右いずれかの方向を向いていて,B君の右手が届く範囲はB君の向いている方向に対して正面,斜め右前,右,斜め右後ろの4マスのみである. B君は,次のいずれかの行動を繰り返す.ただし,これらを同時に行うことは出来ない.
- 前方に壁がない場合,1マス進む.
- 向いている方向を90度右に変える.
- 向いている方向を90度左に変える.
- 右手が接するマスを変える.ただし,この時にB君は右手を離すことが出来ないので,変更前のマスと変更後のマスの間には共通した点を持っていなくてはならない.
Input
入力は以下の形式で与えられる.
$N$ $M$
$S_1$
$S_2$
:
:
$S_N$
$S_i$ ($1 \le i \le N$) は, $M$ 文字の文字列で各文字は次を表す.
- "^","v","<",">"はB君の最初の位置と最初に向いている方向(上下左右の向き)を表す.
- "." は,何もないマスである.B君は,このマスの上を移動することができる.
- "#" は,壁を表す.壁の上を移動することは出来ない.
- "G" はAさんの家の位置を表す.B君は,Aさんの家にたどり着くまで移動を繰り返す.
Constraints
- $1 \le N \le 50$
- $1 \le M \le 50$
- 入力には,文字 "^","v","<",">" のうちいずれかが必ず一つのみ現れる.
- 同様に,入力には,文字 "G" が必ず一つのみ現れる.
- 初期状態では,B君が向いている方向から右の壁にB君の右手が接している.
Output
一度も右手を離さずにAさんの家に辿り着くことが出来る場合には,Aさんの家にたどり着くまでに通った異なるマスの数の最小値を出力せよ. Aさんの家に辿り着くことが出来ない場合には,-1を出力せよ.
Sample Input 1
3 3 G## .#. .<.
Output for the Sample Input 1
4
Sample Input 2
3 3 G## .#. .>.
Output for the Sample Input 2
6
Sample Input 3
3 3 ... .G. .>.
Output for the Sample Input 3
-1
Sample Input 4
4 4 .... .#.G ...# ^#..
Output for the Sample Input 4
8
Time Limit: 2 sec / Memory Limit: 128 MB
Problem Statement
西暦20XX年,学校対抗魔法競技大会が開かれていた.大会もいよいよ,最終競技を残すのみとなった.あなたはその競技の選手の1人である.
あなたが出場する競技は,空間内に配置された青いオブジェをすべて破壊するまでの時間を競うというものである.選手は競技用の銃の持込が許可されている.空間内には複数の青いオブジェと同じ数の赤いオブジェ,そして複数の障害物が配置されている.青いオブジェと赤いオブジェは1対1に対応しており,赤いオブジェが配置されている座標から青いオブジェに弾を撃つことで青いオブジェを破壊しなければならない.空間内に配置されている障害物は球状であり,少しずつ組成が異なっているが,通常の弾であれば障害物に触れると弾はその場に止まってしまう.
競技に使われる弾はMagic Bulletという特殊な弾である.この弾は魔力をため込むことができ,弾が障害物に接触した際に自動的に魔力を消費し,弾が貫通する魔法が発動する.障害物の組成の違いから,貫通するために必要な魔法やその発動のために消費する魔力の量は異なっている.このため,ある障害物に対する魔法が発動した後であっても,別の障害物を貫通するためには新たに別の魔法を発動する必要がある.また,弾が複数の障害物に同時に接触した場合は同時に魔法が発動する.弾に込められた魔力の量は魔法の発動のたびに減少する.
障害物の位置や大きさ,貫通する魔法の発動に必要な魔力の量はすでに公開されているのに対し,赤いオブジェ,青いオブジェの位置は公開されていない.しかし,過去の同一競技の情報から,ある程度オブジェの位置を予想することができた.魔力を弾にこめることは非常に体力を消耗してしまうため,あなたは魔力をできるだけ節約したいと考えた.そこで,赤いオブジェとそれに対応する青いオブジェの位置を仮定して,そのときに弾にこめるべき必要な魔力の最小量,つまり,青いオブジェに到達している時点で弾に残っている魔力が0になる魔力の量を求めよう.
Input
入力はすべて整数である.それぞれの数は1つの空白により区切られる.
$N\ Q$
$x_1\ y_1\ z_1\ r_1\ l_1$
:
:
$x_N\ y_N\ z_N\ r_N\ l_N$
$sx_1\ sy_1\ sz_1\ dx_1\ dy_1\ dz_1$
:
:
$sx_Q\ sy_Q\ sz_Q\ dx_Q\ dy_Q\ dz_Q$
- $N$ は障害物の個数であり,$Q$ は仮定した青いオブジェと赤いオブジェの座標の組の個数である.
- $x_i, y_i, z_i$ はそれぞれ $i$ 個目の障害物の中心の位置を表すx座標,y座標,z座標である.
- $r_i$ は $i$ 個目の障害物の半径である.
- $l_i $ は $i$ 個目の障害物を貫通するための魔法で消費する魔力の量である.
- $sx_j, sy_j, sz_j$ はそれぞれ $j$ 番目の仮定における赤いオブジェの位置を表すx座標,y座標,z座標である.
- $dx_j, dy_j, dz_j$ はそれぞれ $j$ 番目の仮定における青いオブジェの位置を表すx座標,y座標,z座標である.
Constraints
- $0 \leq N \leq 50$
- $1 \leq Q \leq 50$
- $-500 \leq x_i,y_i,z_i \leq 500$
- $1 \leq r_i \leq 1{,}000$
- $1 \leq l_i \leq 10^{16}$
- $-500 \leq sx_j,sy_j,sz_j \leq 500$
- $-500 \leq dx_j,dy_j,dz_j \leq 500$
- 障害物が他の障害物にめり込んでいることはない
- オブジェの座標は障害物の内部,表面にはない
- それぞれの仮定において,赤いオブジェと青いオブジェの座標は一致しない
Output
それぞれ1組の赤いオブジェとそれに対応する青いオブジェの位置の仮定において,空間中に障害物と赤いオブジェと青いオブジェ1対とのみがあるものとして,弾にこめるべき魔力の量を1行に出力せよ.弾は赤いオブジェの位置から青いオブジェの位置まで一直線に飛ぶものとし,弾の大きさは非常に小さいので点として扱う.
Sample Input 1
5 1 0 10 0 5 2 0 20 0 5 12 0 30 0 5 22 0 40 0 5 32 0 50 0 5 42 0 0 0 0 60 0
Output for the Sample Input 1
110
Sample Input 2
1 1 10 5 0 5 9 0 0 0 9 12 0
Output for the Sample Input 2
9
Sample Input 3
5 5 -38 -71 -293 75 1 -158 -38 -405 66 1 -236 -303 157 266 1 316 26 411 190 1 207 -312 -27 196 1 -50 292 -375 -401 389 -389 460 278 409 -329 -303 411 215 -220 -200 309 -474 300 261 -494 -87 -300 123 -463 386 378 486 -443 -64 299
Output for the Sample Input 3
0 2 1 3 0
Time Limit: 4 sec / Memory Limit: 128 MB
Problem Statement
2014年春,ある学生は無事大学に合格し,一人暮らしを始める事となった.ここで問題となるのが夕食をどうするかである.彼はこれから $N$ 日間の夕食の計画を立てる事にした.
彼は $N$ 日間で得られる幸福度の合計を出来る限り大きくしたい.もちろん,美味しいものや好きなものを食べるほど幸福度は高い.
彼の夕食の選択肢は2つ,近くの食堂に向かうか,自炊をするかのどちらかである.
食堂で得られる幸福度は,その日のメニューによって変わる.メニューは日替わりだが毎日一種類のみで,$N$ 日間のメニューは全て既に公開されている.なので,彼は $i$ 日目 ($1 \leq i \leq N$) に食堂に行けば $C_i$ の幸福度を得られるという情報を全て知っている.
自炊で得られる幸福度は,その自炊の開始時点での自炊パワーに定数 $P$ を掛けたものである.自炊パワーは初期値が $Q$ であり,毎日,食堂に行けば-1,自炊をすれば+1,その日の食事の終了時に変動する.
彼のために幸福度の総和の最大値を求めよう.
Input
入力は以下の形式で $N+1$ 行で与えられる.
$N$ $P$ $Q$
$C_1$
$C_2$
:
:
$C_N$
- 1行目は3つの整数 $N, P, Q$ が与えられ,それぞれ日数,自炊の幸福度を算出するための定数,自炊パワーの初期値である.
- 2行目から $N+1$ 行目にはそれぞれ整数が1つずつ与えられ,$i+1$ 行目では $i$ 日目に食堂に行った時に得られる幸福度が与えられる.
Constraints
- $1 \leq N \leq 500{,}000$
- $0 \leq P \leq 500{,}000$
- $ |Q| \leq 500{,}000$
- $ | C_i | \leq 500{,}000$
Output
幸福度の取りうる最大値を一行に出力せよ.
Sample Input 1
1 1 1 2
Output for the Sample Input 1
2
- 考えるべき予定は1日だけである.食堂に行けば2,自炊すると1の幸福度なので,答えは2となる.
Sample Input 2
3 2 1 3 3 3
Output for the Sample Input 2
12
- このケースでは毎日自炊をするのが最適で,幸福度は $2 \times 1+2 \times 2+2 \times 3 = 12$となる.
Sample Input 3
3 1 -1 2 -3 2
Output for the Sample Input 3
2
- 2日目のみで自炊をすることが最善となる.
Sample Input 4
3 1 -10 -10 -10 -10
Output for the Sample Input 4
-27
- 答えが負になることもある.いくらまずくても夕食は食べなければならない.
Time Limit: 2 sec / Memory Limit: 128 MB
Problem Statement
問題文を訂正しました(11:18)
問題文とサンプル入出力について,壊れていた一部の記号の表記を訂正しました(11:58)
盤面上にロボットと壁,ゴールが設置されており, ロボットの行動パターンを記述したプログラムが与えられる.
与えられるプログラムは以下のEBNFで表される.
プログラム := {文};
文 := if文|while文|動作文;
if文 := "[", 条件, プログラム, "]";
while文 := "{", 条件, プログラム, "}";
動作文 := "^"|"v"|"<"|">";
条件 := ["~"], "N"|"E"|"S"|"W"|"C"|"T";
「プログラム」は複数の「文」から0個以上の「文」からなり,1つ以上の文が存在する場合は1つ目の文から順番に1つずつ文が実行される.「文」は「動作文」,「if文」,「while文」のいずれかである.「動作文」は"^", "v","<",">"のいずれかであり,それぞれ以下の動作が実行される.
- "^": 前進
- "v": 後退
- "<": 左に90度回転
- ">": 右に90度回転
「if文」は"[",「条件」,「プログラム」,"]"を順番に並べたもので,以下の手順で実行される.
- 「条件」の内容が真かどうか判定する
- 判定が真なら「プログラム」の内容を実行し,このif文の処理を終了する
- 判定が偽ならこのif文の処理を終了する
「while文」は"{",「条件」,「プログラム」,"}"を順番に並べたもので,以下の手順で実行される.
- 「条件」の内容が真かどうか判定する
- 判定が真なら「プログラム」の内容を実行し,1に戻る
- 判定が偽なら,このwhile文の処理を終了する
「条件」は"N", "E", "S", "W", "C", "T"のいずれかであり,先頭には"~"をつけることができる.それぞれの記述は以下の真偽値を表す.
- 先頭に"~"が付いている場合は真偽値が逆転
- "N": 北を向いているならば真,そうでなければ偽
- "E": 東を向いているならば真,そうでなければ偽
- "S": 南を向いているならば真,そうでなければ偽
- "W": 西を向いているならば真,そうでなければ偽
- "C": 目の前に壁があるならば真,そうでなければ偽
- "T": 常に真
ロボットは最初,北を向いているものとする.ロボットは壁を通ることができず,何もないマスのみを移動できる.もし,プログラムが壁の上を通るような動作を実行しようとした場合,ロボットは移動せずその場にとどまる.最後に,ロボットはゴールに到達した時,実行途中のプログラムが残っていたとしてもすべて中断して動作を停止する.
このとき,ロボットがゴールにたどり着くまでにどのぐらい時間がかかるのか知りたい.ロボットは条件判定やプログラムの読み込みに関しては非常に高速に実行できるので実際の動作時間を決定するのは「動作文」のみである. そこで,このロボットがゴールに辿り着くまでに「動作文」を何回実行するかを教えてほしい.
なお,壁の上を通るような動作を実行しようとして,実際には「動作文」の動作が行われなかった場合にも「動作文」は実行されたものとみなす.
Input
入力は以下の形式で与えられる.
$H$ $W$
$a_{1,1}a_{1,2} \ldots a_{1, W}$
$a_{2,1}a_{2,2} \ldots a_{2, W}$
:
:
$a_{H,1}a_{2,2} \ldots a_{H, W}$
$s$
$H$ は盤面の高さ,$W$ は盤面の幅を表す.
次に盤面を真上から見た状態が与えられる.この盤面は上,下,左,右がそれぞれ北,南,西,東に対応する. 各マスの状態を表す $a_{i,j}$ は以下のいずれかの文字である.
- "s": ロボット(ロボットの初期位置.このマスには壁がないことが保証されている)
- "g": ゴール
- "#": 壁(ロボットは壁の上を移動することはできない)
- ".": 何もないマス
$s$ にはロボットに与えられるプログラムが文字列として入力される.
Constraints
- $1 \leq H, W \leq 50$
- $1 \leq s$ の文字数 $\leq 1{,}000$
- $a_{i, j}$ は".", "#", "s", "g" のいずれか
- "s", "g"はそれぞれ1回しか登場しない
- $i = 1$ または $i = H$ または $j = 1$ または $j = W$ ならば $a_{i,j}$="#"(盤面の外周は壁で囲まれていることが保証されている)
- $s$ として与えられるプログラムは構文的に正しい
Output
たどり着ける場合は "到達するまでに実行した「動作文」の数" を,たどりつけない場合は "-1" を出力せよ.なお,壁の上を通るような動作を実行しようとして,実際には「動作文」の動作が行われなかった場合にも「動作文」が実行されたものとみなす点に注意せよ(入力例1).
Sample Input 1
5 3 ### #g# #.# #s# ### ^<^<vv
Output for the Sample Input 1
5
Sample Input 2
5 7
#######
#.#g..#
#.###.#
#s....#
#######
{T{~C^}<}
Output for the Sample Input 2
17
Sample Input 3
5 7
#######
#.#g..#
#.###.#
#s....#
#######
{T{~C^}>}
Output for the Sample Input 3
-1
Time Limit: 4 sec / Memory Limit: 128 MB
Problem Statement
文字列 $S$ と, $m$ 個のクエリが与えられる. $i$ 番目のクエリは二つの文字列 $x_i,y_i$ で与えられる.
各クエリについて,文字列 $S$ の部分文字列であり, $x_i$ で始まり $y_i$ で終わるものの中で,最長の長さを答えよ.
文字列 $S$ について, $|S|$ は $S$ の長さを表す. また,文字列 $T$ が文字列 $S$ の部分文字列であるとは,ある整数 $i$ が存在して、 $1 \le j \le |T|$ に対して $T_j = S_{i+j}$ を満たすことを言う.ただし $T_j$ は $T$ の $j$ 番目の文字を表す.
Input
入力は以下の形式で与えられる.
$S$
$m$
$x_1$ $y_1$
$x_2$ $y_2$
:
:
$x_m$ $y_m$
- 1行目には,文字列 $S$ が与えられる.
- 2行目には,クエリの個数 $m$ が与えられる.
- 3行目からの $m$ 行のうち $i$ 行目には $i$ 番目のクエリ文字列 $x_i,y_i$ が空白区切りで与えられる.
Constraints
- $1 \le |S| \le 2 \times 10^5 $
- $1 \le m \le 10^5$
- $1 \le |x_i|,|y_i|$
- $\sum_{i=1}^m (|x_i|+|y_i|) \le 2 \times 10^5$
- $S$ 及び $x_i,y_i$ は,半角の英小文字のみからなる.
Output
以下の形式で最大の部分文字列の長さを答えよ.
$len_1$
$len_2$
:
:
$len_m$
1行目からの $m$ 行のうち $i$ 行目には, $i$ 番目のクエリについて,条件を満たす最長の部分文字列の長さ $len_i$ を出力せよ. そのような部分文字列がない場合,0を出力せよ.
Sample Input 1
abracadabra 5 ab a a a b c ac ca z z
Output for the Sample Input 1
11 11 4 3 0
文字列$S$として,abracadabraが与えられる.
- "ab"で始まり"a"で終わる部分文字列は,"abra"や"abraca","abracada","abracadabra"の4種類があるが,最長の部分文字列は"abracadabra"で,長さは11である.
- "a"で始まり"a"で終わる最長の部分文字列も同様に"abracadabra"で,長さは11である.
- "b"で始まり"c"で終わる最長の部分文字列は"brac"で,長さは4である.
- "ac"で始まり"ca"で終わる最長の部分文字列は"aca"で,長さは3である.
- "z"で始まり"z"で終わる部分文字列は存在しない.よって0を出力する.
Sample Input 2
howistheprogress 4 ist prog s ss how is the progress
Output for the Sample Input 2
9 12 5 11
Sample Input 3
icpcsummertraining 9 mm m icpc summer train ing summer mm i c i i g g train i summer er
Output for the Sample Input 3
2 10 8 0 4 16 1 6 6
Time Limit: 2 sec / Memory Limit: 128 MB
Problem Statement
コンテスト中は下記の問題文で出題されましたが、ジャッジ解では同時に複数個アイテムを所持しなければいけない場合を見逃していました。このケースに対して今回の問題の制約で時間内に解くことはおよそ不可能だと思われます。不適切な出題となって申し訳ありませんでした。
当問題担当者としては、下記問題に対して「同時に所持できるアイテムが1個である」という制約を入れれば適切な出題となったと考えています。(9/15 17:47)
中野さんの住む世界では,自分の作った道具で穴を掘り,洞窟を探検することがブームになっている.
道具は $M$ 種類存在し,鉄鉱石を加工することで作ることができる. いくつかの道具は鉄鉱石だけで作ることができるが,道具によっては鉄鉱石に加え,別の道具を利用しないと作れないものもある. また,一部の道具は,いったん他の道具の作成に使うと壊れてしまい,そのままでは利用できなくなる.
壊れているかいないかに関わらず,道具を分解すると鉄鉱石に戻り,他の道具の材料として再利用できる. ただし,分解によって得られる鉄鉱石の量は,その道具を作るのに必要とした鉄鉱石の量よりも減ってしまう.
中野さんは探検のためにどうしても欲しい道具があり,今持っている $N$ 個の鉄鉱石から作れないかと考えている. 残念なことに,中野さんの住む世界では,特別な道具がないとコンピュータを作ることができない. あなたの仕事は,中野さんの代わりに,欲しい道具が作れるかどうかを判定することである.
Input
入力は以下の形式で与えられる.
$M$ $N$ $K$
$a_1$ $b_1$ $c_1$ $d_1$
$s_{1,1}$ $v_{1,1,1}$ $v_{1,1,2}$ ... $v_{1,1,s_{1,1}}$
$s_{1,2}$ $v_{1,2,1}$ $v_{1,2,2}$ ... $v_{1,2,s_{1,2}}$
:
:
$s_{1,d_{1}}$ $v_{1,d_{1},1}$ $v_{1,d_{1},2}$ ... $v_{1,d_{1},s_{1,d_{1}}}$
$a_2$ $b_2$ $c_2$ $d_2$
:
:
$a_M$ $b_M$ $c_M$ $d_M$
$s_{M,1}$ $v_{M,1,1}$ ... $v_{M,1,s_{M,1}}$
:
:
$s_{M,d_{M}}$ $v_{M,d_{M},1}$ $v_{M,d_{M},2}$ ... $v_{M,d_{M},s_{M,d_{M}}}$
1行目には,3つの数 $M, N, K$ が与えられる. $M$ は作れる道具の種類数,$N$ は中野さんが持っている鉄鉱石の数,$K$ は中野さんが手に入れたい道具の番号である.
続く行には,1番目から $M$ 番目までの道具の情報が順番に与えられる. 各道具の情報は,$a_i$, $b_i$, $c_i$, $d_i$ の4つの数を含む行から始まる. $a_i$ はこの道具を作成するために必要な鉄鉱石の個数, $b_i$ はこの道具を分解した時に得られる鉄鉱石の個数を表す.
$c_i = 0$ のとき,$i$ 番目の道具は1回使うと壊れてしまう. $c_i = 1$ のときは,何回でも使うことができる.
続く $d_i$ 行には,この道具を作るために必要となる道具の組み合わせが,1行に1つ与えられる. これらの行は,必要な道具の個数 $s_{i,j}$ から始まり,$s_{i,j}$ 個の数 $v_{i,j,1}, v_{i,j,2}, \cdots, v_{i,j,s_{i,j}}$ がその後に続く. $v_{i,j,k}$ は,道具 $i$ を作るために必要となる道具の組み合わせである. これらの道具をすべて所持していないと,$i$ 番目の道具を作成することはできない. また, $d_i$ 個の組み合わせのうち,どれか1つでも満たしていれば,道具 $i$ を作ることができる. $d_i = 0$ のとき,道具 $i$ は他の道具を使わずに作ることができる.
Constraints
- $1 \le M \le 18$
- $0 \le N \le 10^6$
- $1 \le K \le M$
- $1 \le b_i < a_i \le 10^6$
- $0 \le d_{i} \le 3$
- $1 \le v_{i,j,k} \le M$
- $v_{i,j,k} \neq v_{i,j,k'} \quad\text{if}\, k \neq k'$
Output
$K$ 番目の道具が作成可能なら yes ,そうでないなら no と出力せよ.
Sample Input 1
4 10 4 4 3 0 0 4 3 0 0 2 1 0 1 1 2 2 1 0 1 2 1 3
Output for the Sample Input 1
yes
Sample Input 2
4 8 4 4 3 1 0 4 3 0 0 2 1 0 1 1 2 2 1 0 1 2 1 3
Output for the Sample Input 2
no
Sample Input 3
4 8 4 4 3 1 0 4 3 0 0 2 1 0 2 1 1 1 2 2 1 0 1 2 1 3
Output for the Sample Input 3
yes
Sample Input 4
5 10 4 5 4 1 0 5 1 1 0 5 1 0 1 1 2 6 1 0 2 1 5 2 3 1 3 2 0 1 1 1
Output for the Sample Input 4
yes
Sample Input 5
2 10 2 5 1 0 1 1 2 5 1 0 1 1 1
Output for the Sample Input 5
no
Time Limit: 2 sec / Memory Limit: 128 MB
Problem Statement
今年も,全国プログラミング選手権大会の時期がやってきた. 全国大会の参加権を賭けた地区大会は, $2^n$ チームが1対1の勝ち残り式トーナメント方式で対決する.
トーナメント表にはチーム番号 $0,\ldots,2^n-1$ が割り振られており,1回戦から $n$ 回戦までの対決手順は次の通りである.
- 1回戦では,(チーム番号が $l$ のチーム)と(チーム番号が $l+1$ のチーム)が対決する.($l \equiv 0 ~(\bmod~2)$)
- $i+1$ 回戦($1 \le i < n$)では,「チーム番号が $l$ 以上 $l+2^i$ 未満のチームのうち, $i$ 回戦までの対決で1回も負けていないチーム」と「チーム番号が $l+2^i$ 以上 $l+2^{i+1}$ 未満のチームのうち, $i$ 回戦までの対決で一回も負けていないチーム」が対決する.($l \equiv 0~(\bmod~2^{i+1})$)
$n$ 回戦まで終わると,各チームの順位は $2^{n-(\text{そのチームが勝った回数})}$ 位で確定する. なお,この対決には引き分けが存在しないため,対決したチームのいずれか一方が勝ち,もう一方が負ける.
晴れて地区大会の代表に選ばれた私達は,他の地区大会の結果をマネージャーに調べてもらうことにした. ここで調べてもらった結果が「マネージャーから受け取った順位表」であった. 「マネージャーから受け取った順位表」をより詳細に説明すると,長さ $2^n$ の数列で $i$ ( $ 0 \leq i \leq 2^n -1 $ )番目の要素に チーム番号 $i$ のチームの順位が書かれているものである.
だが,「マネージャーから受け取った順位表」には同じ順位が大量に並んでいた! トーナメントのルール上,同じ順位が大量に並ぶなんてありえないはずだ. そこで,「マネージャーから受け取った順位表」を「無矛盾な順位表」にするために順位を変更するチーム数の最小値を計算してどのくらい順位表が間違っているかをマネージャーに教えてあげよう.
「無矛盾な順位表」とは,順位が確定したトーナメントの結果として起こりうる順位表のことを表す.
Input
入力には,「マネージャーから受け取った順位表」が以下の形式で与えられる.
$n$ $m$
$a_0$ $a_1$ ... $a_m$
$b_0$ $b_1$ ... $b_{m-1}$
- 1行目は $n,m$ の2個の整数からなり, $2^n$ は「地区大会の参加チーム数」, $m$ は「『マネージャーから受け取った順位表』で連続した順位が並んでいる区間の個数」を表す.
- 2行目は $a_i(0 \le i \le m)$ の $m+1$ 個の整数からなり,各 $a_i$ は「『マネージャーから受け取った順位表』で連続した順位が並んでいる区間の区切り位置」を表す.
- 3行目は $b_i(0 \le i < m)$ の $m$ 個の整数からなり,各 $2^{b_i}$ は「『マネージャーから受け取った順位表』におけるチーム番号が $a_i$ 以上 $a_{i+1}$未満のチームの順位」を表す.
Constraints
- $1 \le n \le 30$
- $1 \le m \le 10{,}000$
- $0=a_0 < a_1 < \cdots < a_{m-1} < a_m = 2^n$
- $0 \le b_i \le n$
Output
「マネージャーから受け取った順位表」を「無矛盾な順位表」にするために順位を変更するチーム数の最小値を1行に出力せよ.
Sample Input 1
1 1 0 2 1
Output for the Sample Input 1
1
参加チーム数が2の「無矛盾な順位表」は,{"チーム番号0のチームの順位","チーム番号1のチームの順位"}として $\{1,2\}$ と $\{2,1\}$ の2通りがある. 順位表 $\{2,2\}$ を「無矛盾な順位表」に修正するためには,いずれかのチームの順位を1に変更しなければならない.
Sample Input 2
2 3 0 1 2 4 0 1 2
Output for the Sample Input 2
2
Sample Input 3
2 3 0 1 3 4 0 2 1
Output for the Sample Input 3
0
Sample Input 4
4 5 0 1 2 4 8 16 0 1 2 3 4
Output for the Sample Input 4
10
Time Limit: 2 sec / Memory Limit: 128 MB
Problem Statement
閉路のない連結な有向グラフが与えられる.(有向グラフが連結であるとは,これを無向グラフとした時に連結であるという事である.)
このグラフに対して一つの頂点を選んで首都 $s$ を定めたい.
$T(v)$ = "$v$ から全ての点を到達可能にするために必要な「辺の反転」操作の回数の最小値"とする.
ただし,「辺の反転」とは,頂点 $v,u$ に関して $(v,u)$ に張られていた有向辺を削除して $(u,v)$ に張り直すことである.
頂点 $s$ が首都であるとは任意の頂点 $v$ に対して, $T(s)\leq T(v)$ が成立することである.
首都であるような頂点をすべて列挙して答えよ.
Input
入力は以下のような形式で $M+1$ 行で与えられる.
$N$ $M$
$a_1$ $b_1$
:
:
$a_M$ $b_M$
- 1行目には二つの整数 $N$, $M$ が与えられ,与えられるグラフは $N$ 頂点 $M$ 辺であることを表す.
- 2行目から $M+1$ 行目にはそれぞれ二つの整数 $a_i, b_i$ が与えられ,$a_i$ から $b_i$ に有向辺が張られていることを表す.
Constraints
- $1 \leq N \leq 10{,}000$
- $0 \leq M \leq 100{,}000$
- $0 \leq a_i \leq N-1 $
- $0 \leq b_i \leq N-1 $
- $a_i \neq b_i$
- $i \neq j $ ならば $(a_i, b_i) \neq (a_j, b_j)$
- 与えられるグラフは連結で閉路はない.
- 与えられるグラフに対して,入次数が0である頂点の個数は50以下である.
Output
以下の形式で2行で出力せよ.
$cnum$ $cost$
$c_1$ $c_2$ ... $c_{cnum}$
- 1行目には二つの整数 $cnum$, $cost$ を空白区切りで出力せよ.
- 2行目には $cnum$ 個の整数 $c_i$ を空白区切りで出力せよ.
- 変数の意味は以下の通りである.
- $cnum$ : 首都の性質を満たす頂点数
- $cost$ : 首都となる頂点 $v$ に対する $T(v)$ の値
- $c_i$ : 首都の性質を満たす頂点を番号に関して昇順に並べた時,$i$ 番目の頂点番号
Sample Input 1
3 2 0 1 2 1
Output for the Sample Input 1
2 1 0 2
- 頂点0を首都とするときには辺(2,1)を反転すれば,(0,1), (1,2)の辺を持つグラフができるので1が答え.
- $T(0)=1$,$T(1)=2$,$T(2)=1$である.
Sample Input 2
5 4 0 1 2 1 2 3 4 3
Output for the Sample Input 2
3 2 0 2 4
Sample Input 3
5 5 0 1 1 2 3 2 3 4 4 1
Output for the Sample Input 3
2 1 0 3
Time Limit: 2 sec / Memory Limit: 128 MB
Problem Statement
太郎君はVongressと呼ばれるゲームが大好きである. Vongressとは,$n$ 頂点からなる凸多角形である盤の上で行われる陣取りゲームである.
このゲームでは,$m$ 人のプレイヤーが,盤の内側にそれぞれ1つ駒を置く. 駒の位置は $x$ 座標と $y$ 座標の組で表され,駒の大きさは考えない.
あるプレイヤーの陣地とは,盤上でその人が置いた駒が最も近くにあるような場所からなる領域である. プレイヤーは,自分の陣地の面積をスコアとして得る.
太郎君はいつも盤の形状,置かれた駒の位置,各プレイヤーのスコアを記録していたが, ある日うっかり駒の位置を記録するのを忘れてしまった. そこで太郎君は,盤の形状とプレイヤーの得点から,矛盾のない駒の位置を書き加えることにした.
あなたの仕事は,太郎君に代わって各プレイヤーの得点と矛盾しない駒の位置を求めることである.
Input
入力は以下の形式で与えられる.
$n$ $m$
$x_1$ $y_1$
$x_2$ $y_2$
:
:
$x_n$ $y_n$
$r_1$
$r_2$
:
:
$r_m$
$n$ は盤である凸多角形の頂点数,$m$ はプレイヤーの数を表す. $(x_i,y_i)$ は盤の頂点の座標を表す. $r_1,\ldots,r_m$ は各プレイヤーが得たスコアの比を表す.
Constraints
- $3\le n \le 100$
- $1\le m \le 100$
- $-10^4 \le x_i,y_i \le 10^4$
- $1\le r_j \le 100$
- 入力は全て整数である.
- 凸多角形の頂点 $(x_i,y_i)$ は反時計回りの順番で与えられる.
Output
$m$ 個の駒の位置を以下の形式で出力せよ.
$x'_1$ $y'_1$
$x'_2$ $y'_2$
:
:
$x'_m$ $y'_m$
$(x'_k,y'_k)$は,$k$番目のプレイヤーの駒の位置である.
出力は次の条件を満たさなければならない.
- 駒が凸多角形の内側にある.境界線上にあってもよい.
- どの2つの駒も $10^{-5}$ 以上距離が離れている.
- 与えられる凸多角形の面積を $S$ とする. 出力から求まる $k$ 番目のプレイヤーの陣地の面積について, $\frac{r_k}{r_1+\cdots+r_m}S$ との絶対誤差または相対誤差が $10^{-3}$ 未満である.
Sample Input 1
4 5 1 1 -1 1 -1 -1 1 -1 1 1 1 1 1
Output for the Sample Input 1
0.0000000000 0.0000000000 0.6324555320 0.6324555320 -0.6324555320 0.6324555320 -0.6324555320 -0.6324555320 0.6324555320 -0.6324555320
下図のように駒を配置すれば,全プレイヤーが同じスコアを得られる. 黒い線分が盤,赤い点がプレイヤーの駒,青い線分がプレイヤーの陣地の境界線をそれぞれ表す.

Sample Input 2
4 3 1 1 -1 1 -1 -1 1 -1 9 14 9
Output for the Sample Input 2
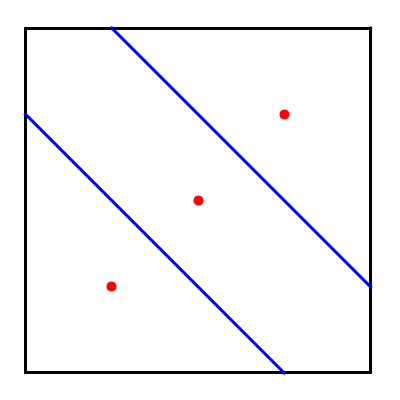
-0.5 -0.5 0 0 0.5 0.5
下図のように駒を配置すればよい.
Sample Input 3
8 5 2 0 1 2 -1 2 -2 1 -2 -1 0 -2 1 -2 2 -1 3 6 9 3 5
Output for the Sample Input 3
1.7320508076 -0.5291502622 1.4708497378 -0.2679491924 -0.4827258592 0.2204447068 -0.7795552932 0.5172741408 -1.0531143674 0.9276127521
下図のように駒を配置すればよい.
