G - Escape
Editorial
 /
/ 
入力は以下の形式で標準入力から与えられる。
答えを1行に出力せよ。
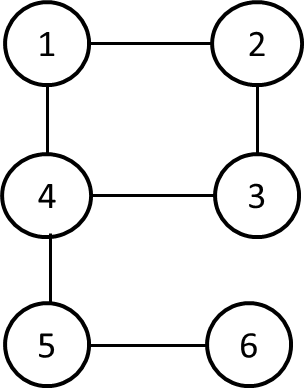
頂点 1→2→3→4→5→6 と進むことで全ての頂点の点数を集めることができます。
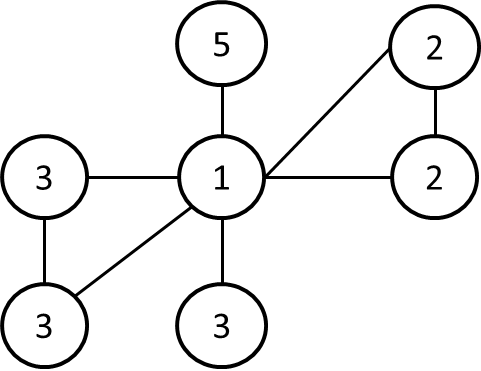
頂点 1→2→3→1→5→6→1→4 と進むことで16点を集めることができます。
 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
Problem Statement
(13:35) Input format の記述を一部修正しました
頂点に正の値を持つ無向グラフが与えられる。 頂点には 1 から N の番号がついており、i 番目の頂点は w_i の値を持っている。 1 番目の頂点からスタートし、直前に通った辺を通ることができないという制約のもとでグラフ上を移動することができる。 各頂点では,初めて訪れた時に限りその頂点が持つ値の点数を得られる。
取得できる点数の総和の最大値を求めよ。
Constraints
- 1 \leq N \leq 100000
- N-1 \leq M \leq 100000
- 1 \leq w_i \leq 1000
- 1 \leq u_i, v_i \leq N
- 多重辺・自己辺は存在しない
- グラフは連結である
Input Format
N M w_1 w_2 ... w_N u_1 v_1 u_2 v_2 ... u_M v_M
1 行目にはグラフ(修正 13:36:00)の頂点数 N と辺の数を表す整数 M が入力される。
2 行目には各頂点が持つ値 w_i が入力される。
さらに続けて M 行に、各辺により繋がれる 2 頂点の番号が入力される。
Output Format
Sample Input 1
6 6 1 2 3 4 5 6 1 2 2 3 3 4 1 4 4 5 5 6
Sample Output 1
21

頂点 1→2→3→4→5→6 と進むことで全ての頂点の点数を集めることができます。
Sample Input 2
7 8 1 3 3 5 2 2 3 1 2 2 3 3 1 1 4 1 7 1 5 1 6 5 6
Sample Output 2
16

頂点 1→2→3→1→5→6→1→4 と進むことで16点を集めることができます。