OUPC 2023 Day1 : 大阪大学セット

A - Mijingiri

Time Limit: 2 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

kotamanegi 君をみじんぎりします。

初め、kotamanegi 君は大きさ A の欠片です。あなたは 1 回の切断で 1 つの欠片を 2 つに分けることができます。厳密には、大きさ X の欠片と X 未満の正整数 Y を選び、選んだ欠片を大きさが X-Y と Y の 2 つの欠片に分けることができます。

すべての欠片の大きさを T 以下にするのに必要な最小の切断回数を求めてください。

制約

1 \leq A \leq 100
1 \leq T \leq 100
入力はすべて整数

入力

入力は以下の形式で標準入力から与えられます。

A T

出力

必要な最小の切断回数を 1 行で出力してください。

入力例 1

7 3

出力例 1

大きさ 7 の欠片を大きさ 3 以下の欠片に分けるには、例えば 1 回目の切断で大きさ 7 の欠片を大きさ 3 の欠片と大きさ 4 の欠片に分け、 2 回目の切断で大きさ 4 の欠片を大きさ 2 の欠片と大きさ 2 の欠片に分ければよいです。

1 回のみの切断ですべての欠片を大きさ 3 以下にすることはできないため、答えは 2 となります。

入力例 2

6 3

出力例 2

入力例 3

100 1

出力例 3

B - Gomamayo

Time Limit: 2 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

文字列 S に対して、以下の条件を満たす長さ 1 以上の文字列 A, B が存在するとき、S は「ゴママヨである」と言います。

S は A と B をこの順に結合した文字列に等しく、 A の最後の文字と B の最初の文字が等しい。

例えば、文字列 abba や abbcddc はゴママヨですが、 ababa はゴママヨではありません。

英小文字からなる文字列 S が与えられます。(i, j) (1 \leq i \leq j \leq |S|) であって、 S の i 文字目から j 文字目までを取り出した連続部分文字列がゴママヨであるようなものの個数を 998244353 で割った余り求めてください。

制約

1 \leq |S| \leq 10^{6}
S は英小文字からなる文字列

入力

入力は以下の形式で標準入力から与えられます。

出力

答えを 1 行で出力してください。

入力例 1

abbcc

出力例 1

bb, cc, abb, bbc, bcc, abbc, bbcc, abbcc はゴママヨなので、 (2, 3), (4, 5), (1, 3), (2, 4), (3, 5), (1, 4), (2, 5), (1, 5) は条件を満たします。これら以外の (i,j) は条件を満たしません。

入力例 2

ssss

出力例 2

入力例 3

kotamanegi

出力例 3

C - Caesar Cipher

Time Limit: 2 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

シーザー暗号は 3 文字シフトが一般的ですが、ここでは 0 \leq k < 26 の任意の鍵 k の数だけシフトするものとします。
平文は英小文字からなり、英小文字の範囲でシフトするものとします。

シーザー暗号の詳しい説明

暗号化する前の文を平文、暗号化した文を暗号文と言います。暗号文を平文に戻すことを復号と言います。

鍵を k (0 \leq k < 26) とします。暗号化するときは、各文字を k 個次の文字に変更します。ただし、z の次の文字は a です。

例として、鍵が 2 のときを考えます。平文 ayz を暗号化すると cab となります。

N 個の平文の候補があります。i 個目の候補は S_i で、これらの文字数はすべて M です。

Q 個の暗号文が与えられるので復号してください。j 個目の暗号文は T_j で、平文の候補のうち一つをシーザー暗号を用いて暗号化したものです。それぞれの暗号文は独立に選ばれた鍵を使って、暗号化されています。

平文の候補は暗号化したときに必ず特定できるように定まっています。つまり、S_a と S_b (a \ne b) をそれぞれ任意の鍵 k_a, k_b で暗号化したときの暗号文が一致するようなケースはありません。

制約

1 \leq N \leq 200{,}000
1 \leq M \leq 200{,}000
1 \leq Q \leq 200{,}000
M \max (N, Q) \leq 200{,}000
N, M, Q は整数
S_i, T_j は英小文字からなる長さ M の文字列
平文の候補は暗号化したときに必ず特定できる
T_j は平文の候補のうち一つをシーザー暗号を用いて暗号化したもの

入力

入力は以下の形式で標準入力から与えられます。

N M
S_1
S_2
\vdots
S_N
Q
T_1
T_2
\vdots
T_Q

出力

Q 行出力してください。

j 行目には、j 個目の暗号文 T_j を復号したもの出力してください。

入力例 1

2 3
ayz
bbb
2
cab
aaa

出力例 1

ayz
bbb

鍵を 2 として ayz を暗号化すると cab となります。
鍵を 25 として bbb を暗号化すると aaa となります。

入力例 2

3 7
rainbou
osakauv
atcoder
2
ptblbvw
envaobh

出力例 2

osakauv
rainbou

D - Han Burger

Time Limit: 2 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

N 個の文字あるいは文字列 X_1, X_2, \dots, X_N をこの順に連結させた文字列を X_1 + X_2 + \cdots + X_N と表記します。
文字列に対して、バーガー、全バーガー、半バーガーを以下のように定義します。この定義はE問題と同じです。

バーガーとは、全バーガーである文字列、および半バーガーである文字列
全バーガーとは、あるバーガー A とある文字 c に対して、c + A + c と書ける文字列、および空文字列
半バーガーとは、ある空でないバーガー A、B に対して、A + B と書ける文字列のうち、全バーガーでない文字列

例えば、abba や abbcca は全バーガー、aabb や abbacc は半バーガーですが、abbcbbc や ababa はバーガーではありません。

英小文字からなる文字列 S に対し、S + T が全バーガーとなるような、英小文字からなる文字列 T が存在するとき、|T| が最小である T のうち辞書順で最小のものを出力してください。そのような T が存在しないときは -1 を出力してください。

辞書順とは ?

文字列 S = S_1S_2 \cdots S_{|S|} が文字列 T = T_1T_2 \cdots T_{|T|} より 辞書順で小さい とは、下記の 1. と 2. のどちらかが成り立つことを言います。ここで、|S|, |T| はそれぞれ S,T の長さを表します。

1. |S| < |T| かつ S = S_1S_2 \cdots S_{|S|} = T_1T_2 \cdots T_{|S|}。
2. ある整数 1 \leq i \leq \min\{|S|, |T|\} が存在して、下記の 2 つがともに成り立つ。

S = S_1S_2 \cdots S_{i-1} = T_1T_2 \cdots T_{i-1}
S_i が T_i よりアルファベット順で小さい文字である。

制約

1 \leq |S| \leq 200{,}000
S は英小文字からなる文字列

小課題

( 1 点) S は a と b からなり、|S| \leq 10 となる文字列
( 99 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

出力

答えを 1 行で出力してください。

入力例 1

abcca

出力例 1

aba

T = aba とすると、S+T = abccaaba は全バーガーとなります。
条件を満たす T は aba 以外にも考えられますが、2 文字以下であるものは存在せず、3 文字である T のうち辞書順で最も小さいのは aba であるため、aba を出力します。

このテストケースは小課題 1 の制約を満たしません。

入力例 2

abba

出力例 2

T を空文字列にすれば、S+T = abba は全バーガーとなります。

このテストケースは小課題 1 の制約を満たします。

E - Han Burger 2

Time Limit: 4 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

N 個の文字あるいは文字列 X_1, X_2, \dots, X_N をこの順に連結させた文字列を X_1 + X_2 + \cdots + X_N と表記します。
また、文字列 X の i 文字目から j 文字目までを取り出した連続部分文字列を X[i,j] と表記します。
文字列に対して、バーガー、全バーガー、半バーガーを以下のように定義します。この定義はD問題と同じです。

バーガーとは、全バーガーである文字列、および半バーガーである文字列
全バーガーとは、あるバーガー A とある文字 c に対して、c + A + c と書ける文字列、および空文字列
半バーガーとは、ある空でないバーガー A、B に対して、A + B と書ける文字列のうち、全バーガーでない文字列

例えば、abba や abbcca は全バーガー、aabb や abbacc は半バーガーですが、abbcbbc や ababa はバーガーではありません。

英小文字からなる文字列 S と正の整数 K が与えられます。k = 0, 1, 2, \dots, K について、以下の問に答えてください。

S[i, j] + T が全バーガーとなる、英小文字からなる文字列 T として考えられる長さの最小値が k となる (i, j) (1 \leq i \leq j \leq |S|) の個数を 998244353 で割った余りを求めよ。

制約

1 \leq |S| \leq 200{,}000
1 \leq K \leq 200{,}000
S は英小文字からなる文字列
K は整数

小課題

( 1 点) K \leq 300
( 99 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

S
K

出力

K+1 行出力してください。
i 行目に k = i-1 としたときの答えを出力してください。

入力例 1

abcc
3

出力例 1

S[i,j] + T が全バーガーとなる T について、T の長さの最小値が k (0 \leq k \leq 3) となる (i, j) の組はそれぞれ以下になります。

k = 0 のとき、(3, 4)
k = 1 のとき、(1, 1), (2, 2), (3, 3), (4, 4), (2, 4)
k = 2 のとき、(1, 2), (2, 3), (1, 4)
k = 3 のとき、(1, 3)

S[1, 4] = abcc は、T = ba とすると全バーガーになります。T の長さが 1 以下のときは全バーガーにはなりません。

このテストケースは小課題 1 の制約を満たします。

入力例 2

fortississimo
7

出力例 2

このテストケースは小課題 1 の制約を満たします。

F - Remainder of Max Problem

Time Limit: 2 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

KowerKoint 君は競技プログラミングのコンテストに出場し、そこでは以下の問題が出題されました。

正整数 N と、正整数からなる長さ N の数列 A=(A_1, A_2, \dots, A_N) が与えられる。 A の最大値を正整数 m で割った余りを求めて出力せよ。

KowerKoint 君は A の要素を m で割った余りの最大値を求めて出力するコードを提出しました。これは問題に対して正しいプログラムではありませんが、このコンテストの作問者はテストケースを一つしか用意しなかったため、奇跡的に正解（の値を出力）することができました。作問者が用意したテストケースの N と A が与えられます。クエリが Q 個与えられます。 q 番目のクエリでは m として考えられる正整数のうち、 M_q 以下のものの個数を求めてください。

制約

1 \leq N \leq 200{,}000
1 \leq N \times A_i \leq 2 \times 10^{10}
1 \leq Q \leq 200{,}000
1 \leq M_q \leq 10^{18}
入力はすべて整数

小課題

(1 点) N \leq 100, A_i \leq 100
(99 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

N
A_1 A_2 \dots A_N
Q
M_1
M_2
\vdots
M_Q

出力

Q 行出力してください。 q 行目には、q 番目のクエリに対する答えを出力してください。

入力例 1

出力例 1

3
2

1 つめのクエリの場合、 m として 1,2,4 の 3 通りが考えられます。

このテストケースは小課題 1 の制約を満たします。

入力例 2

出力例 2

1
10
22

このテストケースは小課題 1 の制約を満たします。

G - Impassable Game

Time Limit: 6 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

N 頂点 M 辺の有向グラフ G および正の整数 K が与えられます。
G の頂点および辺には頂点 1, 頂点 2, ..., 頂点 N および辺 1, 辺 2, ..., 辺 M と番号づけられており、辺 i (1 \leq i \leq M) は頂点 u_i から頂点 v_i へ向かう辺で、パラメータ b_i が付加されています。 b_i は 0 または 1 です。

有向グラフ G について、以下の 3 つのことが保証されます。

G は多重辺を持たない。
G はサイクルを持たない。
各頂点は頂点 1 から辺をたどることで到達でき、頂点 1 からの最短経路の長さと最長経路の長さは一致し、それは K 以下である。

2 つの駒を使って、2 人のプレイヤーがゲームを行います。

最初、各プレイヤーは自分の駒を頂点 1 に置く。
プレイヤーは自分のターンになったら以下の操作のどちらかを行う。
- 移動 : 自分の駒をちょうど 1 回移動させる。自分の駒が頂点 i にあるとき、頂点 i から頂点 j へ向かう辺があるような頂点 j へのみ移動させることができる。ただし、自分の駒が頂点 1 にあるときは、移動できる頂点から等確率でランダムに 1 つ選んで移動させなければならない。また、先手のプレイヤーは全ての辺を、後手のプレイヤーは b_i=0 である辺のみを使用することができる。
- 敗北宣言 : 自分の負け、相手の勝ちとしてゲームを終了とする。
先手のプレイヤーから交互にターンを繰り返し、敗北宣言が行われないならば、後手のプレイヤーが移動を K 回行った直後の時点でゲームを終了とする。その時点で 2 つの駒が同じ頂点にあるなら後手の勝ち、異なる頂点にあるなら先手の勝ちとなる。

各プレイヤーは自分の勝ちを目指して最適な戦略を取ります。
先手のプレイヤーが勝つ確率を \bmod 998244353 で求めてください。

確率 \bmod 998244353 の定義

この問題で求める確率は必ず有理数になることが証明できます。また、この問題の制約下では、求める確率を既約分数 \frac{y}{x} で表したときに x が 998244353 で割り切れないことが保証されます。このとき、y≡xz \pmod {998244353} を満たす 0 \leq z < 998244353 がただ一つ存在するので、z を出力してください。

制約

2 \leq N \leq 4{,}000
1 \leq M \leq 2 \times 10^{6}
1 \leq K \leq 4{,}000
1 \leq u_i, v_i \leq N
b_i \in \{0, 1\}
G は多重辺を持たない。
G はサイクルを持たない。
各頂点は頂点 1 から辺をたどることで到達でき、頂点 1 からの最短経路の長さと最長経路の長さは一致し、それは K 以下である。
入力はすべて整数

小課題

(1 点) N\leq100, M\leq1000
(99 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

N M K
u_1 v_1 b_1
u_2 v_2 b_2
\vdots
u_M v_M b_M

出力

先手のプレイヤーが勝つ確率を \bmod 998244353 で出力してください。

入力例 1

出力例 1

499122177

各プレイヤーが駒を 1 回移動させた時点で、先手の駒が存在する頂点を i、後手の駒が存在する頂点を j としたときの組 (i, j) のうち、先手が勝つ組と後手が勝つ組はそれぞれ以下です。

先手が勝つ組 : (2, 3)、(3, 3)
後手が勝つ組 : (2, 2)、(3, 2)

この 4 つの組のうち、(3, 2) が選ばれたとき、以下のような進行が考えられます。

まず頂点 1 に駒を置く。
先手が辺 2 を使用して自分の駒を頂点 3 へ移動させる。
後手が辺 1 を使用して自分の駒を頂点 2 へ移動させる。
先手が辺 6 を使用して自分の駒を頂点 5 へ移動させる。
後手が辺 4 を使用して自分の駒を頂点 5 へ移動させる。
後手が駒を 2 回動かしたのでゲームを終了とする。2 つの駒が頂点 5 に存在するため後手の勝ち

他にもゲームの進行は考えられますが、(3, 2) が選ばれた場合、先手がどのような戦略を取っても後手が勝つことができます。

なお、先手が勝つ確率は \frac{1}{2} と求めることができ、これを \bmod 998244353 で表現すると 499122177 となります。

このテストケースは小課題 1 の制約を満たします。

入力例 2

出力例 2

249561089

先手が勝つ組 : (2, 3)、(3, 2)、(3, 3)
後手が勝つ組 : (2, 2)

この 4 つの組のうち、(3, 2) が選ばれたとき、以下のような進行が考えられます。

まず頂点 1 に駒を置く。
先手が辺 2 を使用して自分の駒を頂点 3 へ移動させる。
後手が辺 1 を使用して自分の駒を頂点 2 へ移動させる。
先手が辺 5 を使用して自分の駒を頂点 5 へ移動させる。
後手が辺 3 を使用して自分の駒を頂点 4 へ移動させる。
後手が駒を 2 回動かしたのでゲームを終了とする。2 つの駒が異なる頂点に存在するため先手の勝ち

他にもゲームの進行は考えられますが、(3, 2) が選ばれた場合、後手がどのような戦略を取っても先手が勝つことができます。

なお、先手が勝つ確率は \frac{3}{4} と求めることができ、これを \bmod 998244353 で表現すると 249561089 となります。

このテストケースは小課題 1 の制約を満たします。

入力例 3

2 1 1
1 2 1

出力例 3

後手は移動を 1 回も行うことなく敗北宣言しなければなりません。

このテストケースは小課題 1 の制約を満たします。

入力例 4

出力例 4

199648871

このテストケースは小課題 1 の制約を満たします。

H - Wonderful Stage

Time Limit: 3 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

KowerKoint 君は音楽ゲームが好きです。 KowerKoint 君は、このゲームのとある曲で、できるだけ簡単にちょうど X のスコアを得たいと考えています。

この曲では M 個のリズムアイコンが流れてきます。KowerKoint 君はこれらのリズムアイコンをそれぞれ 1 回以下の回数タップすることができます。曲の開始時スコアは 0 で、 i 番目のリズムアイコンをタップすると、 S_i のスコアを得ることができます。

また、 1 \leq j \leq K に対し、 a_j 番目から b_j 番目までのリズムアイコンをすべてタップすることの難易度は c_j です。

スコアをちょうど X にできるかを判定し、ちょうど X にできるならば、達成する必要のある難易度の最大値としてありうる最小値を求めてください。ただし、任意の j について a_j 番目から b_j 番目までのリズムアイコンのどれかはタップせずに合計スコアをちょうど X にできる場合、難易度の最大値は 0 とします。

制約

1 \leq X \leq 10{,}000
1 \leq M \leq 1{,}000
1 \leq K \leq \min(200{,}000,\frac{M(M+1)}{2})
1 \leq S_i \leq 10^{9}
1 \leq a_j \leq b_j \leq M
(a_1,b_1),(a_2,b_2),\dots,(a_K,b_K) は相異なる
1 \leq c_i \leq 10^{9}
入力はすべて整数

小課題

( 1 点) a_j=b_j
( 99 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

X M K
S_1 S_2 \dots S_M
a_1 b_1 c_1
a_2 b_2 c_2
\vdots
a_K b_K c_K

出力

スコアをちょうど X にできるならば、達成する必要のある難易度の最大値としてあり得る最小値を 1 行で出力してください。スコアをちょうど X にできない場合は -1 を出力してください。

入力例 1

出力例 1

4 番目以外のリズムアイコンをタップするのが最適です。

このテストケースは小課題 1 の制約を満たしません。

入力例 2

出力例 2

-1

スコアをちょうど 9 にすることはできません。

このテストケースは小課題 1 の制約を満たしません。

入力例 3

出力例 3

このテストケースは小課題 1 の制約を満たします。

I - Min!? Max!? Max!? Min!?

Time Limit: 4 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

正整数 N と長さ M の整数列 A が与えられます。

0 以上 N-1 以下の整数 x に対し、以下の値を f(x) と表します。

\sum\limits_{i=1}^M A_i B_i \equiv x \pmod N となるような長さ M の整数列 B のうち、 \sum\limits_{i=1}^M |B_i| の最小値

なお、制約の条件下で、 \sum\limits_{i=1}^M A_i B_i \equiv x \pmod N となるような整数列 B が存在することが保証されます。x = 0,1, \dots , N-1 のうち、 f(x) が最大となるような x を求めてください。答えが複数ある場合には、そのような x のうち一番小さいものを求めてください。

制約

1 \leq M \leq N \leq 200{,}000
1 = A_1 < A_2 < \dots < A_M \leq N
入力はすべて整数

小課題

(1 点) NM \leq 200{,}000
(99 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

N M
A_1 A_2 \dots A_M

出力

答えを 1 行で出力してください。

入力例 1

4 1
1

出力例 1

f(0)=0,f(1)=1,f(2)=2,f(3)=1 なので答えは 2 になります。

このテストケースは小課題 1 の制約を満たします。

入力例 2

6 2
1 2

出力例 2

このテストケースは小課題 1 の制約を満たします。

J - Sum Sum

Time Limit: 2 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

正整数 N, M および、長さ N の正整数列 a, b が与えられます。 \sum\limits_{k=1}^N \sum\limits_{x=1}^M (a_k x^k + b_k k^x) を 998244353 で割った余りを求めてください。

制約

1 \leq N \leq 200{,}000
1 \leq M \leq 10^{18}
1 \leq a_k \leq 10^{9}
1 \leq b_k \leq 10^{9}
入力はすべて整数

小課題

(1 点) N \leq 100
(1 点) N \leq 5{,}000
(98 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

N M
a_1 a_2 \dots a_N
b_1 b_2 \dots b_N

出力

答えを出力してください。

入力例 1

3 2
2 1 7
5 4 2

出力例 1

答えは (2 \times 1^1+5 \times 1^1) + (2 \times 2^1+5 \times 1^2) + (1 \times 1^2+4 \times 2^1) + (1 \times 2^2+4 \times 2^2) + (7 \times 1^3+2 \times 3^1) + (7 \times 2^3+2 \times 3^2) = 132 です。

このテストケースは小課題 1, 2 の制約を満たします。

入力例 2

5 123456789012345678
180484765 48450102 509940465 587404308 566608826
261439033 751569102 489070200 768834397 292361745

出力例 2

449755530

このテストケースは小課題 1, 2 の制約を満たします。

K - Minimize Transfer Time

Time Limit: 2 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

N 個の空港があり、各空港は 1 から N の番号で表されます。

M 便のフライトがあり、i 番目のフライトは空港 a_i から空港 b_i へ移動し、出発時刻は s_i 、到着時刻は t_i です。空港から空港へはフライトでのみ移動できます。乗り換えにかかる時間は無視できる、つまり乗っていたフライトの到着と同時に出発する別のフライトに乗り換えることが可能であるとします。

空港 1 から空港 N へなるべく移動時間が短くなるように移動するときの移動時間を求めてください。ただし、たどり着く方法が存在しない場合は -1 を出力してください。ここで、移動時間は空港 1 を出発した時刻を S、空港 N に到着した時刻を T として、T - S で表されます。

制約

2 \leq N \leq 200{,}000
0 \leq M \leq 200{,}000
1 \leq a_i, b_i \leq N
0 \leq s_i < t_i \leq 10^{9}
a_i \ne b_i
入力はすべて整数

小課題

( 1 点) a_i = 1 ならば s_i = 0
( 99 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

N M
a_1 b_1 s_1 t_1
a_2 b_2 s_2 t_2
\vdots
a_M b_M s_M t_M

出力

空港 1 から空港 N へなるべく移動時間が短くなるように移動するときの移動時間を 1 行で出力してください。ただし、たどり着く方法が存在しない場合は -1 を出力してください。

入力例 1

出力例 1

時刻 3 に出発して、フライト 2 、フライト 3 に乗ることで時刻 7 に到着します。

このテストケースは小課題 1 の制約を満たしません。

入力例 2

2 0

出力例 2

-1

たどり着く方法が存在しない場合は -1 を出力してください。

このテストケースは小課題 1 の制約を満たします。

入力例 3

出力例 3

乗り換えにかかる時間は無視できます。

このテストケースは小課題 1 の制約を満たします。

L - KowerKoint Doko

Time Limit: 2 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

KowerKoint 君がどこかに行ってしまいました。

(x, y) 座標系において、KowerKoint 君は時刻 0 秒のとき原点 (0, 0) にいたことがわかっています。KowerKoint 君は、1 秒ごとに次のように移動します（移動は瞬時に行われます）。

時刻 1 秒では、KowerKoint 君は (0, 1) に移動します。
時刻 2 秒の移動からは、移動前にいた座標を (x,y) として (x+1,y),(x,y+1),(x-1,y),(x,y-1) の 4 つの座標のうち、1 秒前の移動前にいた座標を除いた 3 つから、等確率に 1 つを選んでそこに移動します。

時刻 T 秒の移動の直後に KowerKoint 君がいる場所の x 座標と y 座標の期待値をそれぞれ X, Y とします。

X, Y をそれぞれ \bmod 998244353 で求めてください。

期待値 \bmod 998244353 の定義

この問題で求める期待値は必ず有理数になることが証明できます。また、この問題の制約下では、求める期待値を既約分数 \frac{y}{x} で表したときに x が 998244353 で割り切れないことが保証されます。このとき、y≡xz \pmod {998244353} を満たす 0 \leq z <998244353 がただ一つ存在するので、z を出力してください。

制約

1 \leq T \leq 10^{18}
入力はすべて整数

小課題

(1 点) T \leq 1000000
(99 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

出力

X, Y をそれぞれ \bmod 998244353 で、この順に空白区切りで 1 行で出力してください。

入力例 1

出力例 1

0 1

このテストケースは小課題 1 の制約を満たします。

入力例 2

出力例 2

0 332748119

このテストケースは小課題 1 の制約を満たします。

M - Can't Be UT

Time Limit: 4 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

xy 平面上にイチョウの葉が N 枚あります。 N 枚のイチョウの葉はすべて円の形をしており、 i 番目のイチョウの葉の中心の座標は(A_i,B_i) で、半径はすべて等しいです。

今からこれら N 枚のイチョウの葉に色を付けます。色を付ける前 KowerKoint 君は落ち着いていますが、色を付け終わったあと以下の条件を満たすような (i,j) (1\leq i < j \leq N) が存在すると落ち着きをなくします。

i 番目のイチョウの葉の内部（周は含まれない）と j 番目のイチョウの葉の内部（周は含まれない）の共通部分が空ではない
i 番目のイチョウの葉の色と j 番目のイチョウの葉の色が異なる

KowerKoint 君はカラフルな風景が好きなので、1 枚以上のイチョウの葉につけられた色の種類数が C 以上になるようにしたいです。このような色の付け方で、色を付け終わったあとも KowerKoint 君が落ち着いていられるようなものが存在するようなイチョウの葉の半径の最大値を求めてください。制約内で、最大値が常に存在することが証明できます。

制約

2 \leq C \leq N \leq 50{,}000
-10{,}000 \leq A_i, B_i \leq 10{,}000
(A_i,B_i) はすべて異なる
入力はすべて整数

小課題

(1 点) N \leq 1{,}000
(99 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

N C
A_1 B_1
A_2 B_2
\vdots
A_N B_N

出力

答えを 1 行で出力してください。

正しい値との絶対誤差または相対誤差が 10^{-6} 以下であるとき、正しいとみなされます。

入力例 1

出力例 1

5.315073

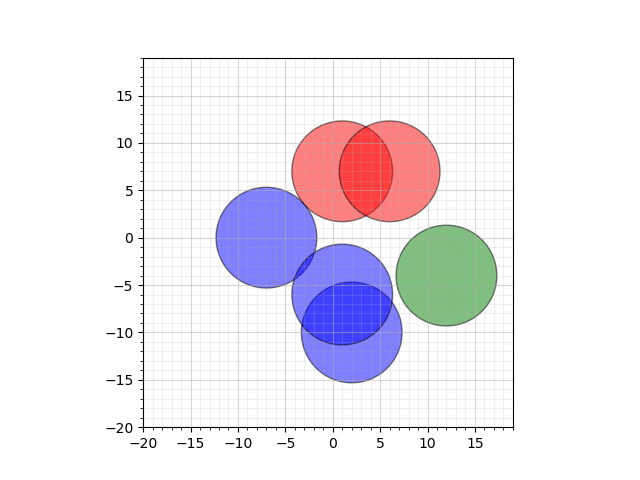
半径が \frac{\sqrt{113}}{2}=5.31507291\dots 以下のとき、下の図のように 3 種類の色をつけることができます。

このテストケースは小課題 1 の制約を満たします。

入力例 2

10 2
3789 5753
-9503 -3197
2918 -1274
-762 5030
-1343 -6275
2936 5844
640 -978
9997 -3756
-633 910
-8076 -6940

出力例 2

3750.752

このテストケースは小課題 1 の制約を満たします。

N - Bench

Time Limit: 2 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

横に長いベンチが 1 つあります。ベンチには 1 から L までの整数が割り当てられた L 個のクッションが一列に並べて置かれており、各 i (1\leq i\leq L-1) についてクッション i とクッション i+1 が隣り合っています。

このベンチに人の集団が、N 個のグループに分かれて順に座りに来ます。 j 番目のグループは A_j 人の人からなり、ベンチの隣り合う A_j 個のクッション（より厳密には、ある p について、クッション p,p+1,\dots,p+A_j-1）に 1 人ずつ座るようにします。隣り合う A_j 個のクッションでそのすべてに人が座っていないものが存在しないとき、そのグループは座るのに失敗します。座るのに失敗したグループがあったとき、それよりあとのグループはベンチに座りに来るのを諦めます。

1 番目のグループがベンチに座りに来る前に、KowerKoint 君は、お金を使ってグループの人数を増減させることができます。具体的には、以下の操作を任意の回数（0 回でも良い）行います。

B_j 円支払い、j 番目のグループの人数を 1 人減らす (j 番目のグループの人数が 2 人以上のときのみ行える）
C_j 円支払い、j 番目のグループの人数を 1 人増やす

ただし、操作の途中や操作後に所持金が負になってはいけません。また、B_j は負であることがあり、-x 円支払うとは x 円受け取るということを表します。

各グループが座る場所をどのように選んでも最終的に合計 y 人以上が必ず座れるような最大の y を考えます。 KowerKoint 君は、このような y を操作によって最大化したいです。整数 Q と非負整数の列 M_1,M_2,\dots,M_Q が与えられるので、各 k (1\leq k\leq Q) について、操作前の所持金が M_k 円であるときの y の最大値を答えてください。

制約

1 \leq N \leq L \leq 3{,}000
1 \leq A_j \leq L
-10^{9} \leq B_j \leq 10^{9}
0 \leq C_j \leq 10^{9}
1 \leq B_j+C_j
1 \leq Q \leq 200{,}000
0 \leq M_k \leq 10^{15}
入力はすべて整数

小課題

(1 点) B_j=1,C_j=1,Q=1,M_k=0
(99 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

N L
A_1 B_1 C_1
A_2 B_2 C_2
\vdots
A_N B_N C_N
Q
M_1
M_2
\vdots
M_Q

出力

Q 行出力してください。 k 行目には、操作前の所持金が M_k 円であるとき、KowerKoint 君の操作によって、座り方によらず必ず座れる人数の最大値を出力してください。

入力例 1

出力例 1

1 番目のクエリでは、KowerKoint 君は 0 円持っています。操作をしない場合、1 番目のグループの 2 人のみ必ず座ることができます。3 番目のグループの人数を好きなだけ増やすことができますが、増やしても必ず座れる人数は増えません。
2 番目のクエリでは、KowerKoint 君は 1 円持っています。1 円支払って 2 番目のグループの人数を 1 人減らすと、2 グループ目までの 2+3=5 人が必ず座ることができ、これが最大です。
3 番目のクエリでは、KowerKoint 君は 5 円持っています。1 円支払って 2 番目のグループの人数を 1 人減らし、3 円支払って 3 番目のグループの人数を 1 人減らすと、2+3+1=6 人すべてが必ず座ることができ、これが最大です。
4 番目のクエリでは、KowerKoint 君は 10 円持っています。2\times5=10 円支払って 1 番目のグループの人数を 5 人増やすと、1 番目のグループの 7 人が必ず座ることができ、これが最大です。

このテストケースは小課題 1 の制約を満たしません。

入力例 2

出力例 2

このテストケースは小課題 1 の制約を満たします。

入力例 3

出力例 3

このテストケースは小課題 1 の条件を満たしません。

O - Special Matrix

Time Limit: 3 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

この問題では以下の数式表現を用います。

M_{i,j} : 行列 M の i 行 j 列成分
\text{GCD}(x,y) : x と y の最大公約数

非負整数を成分とする N 行 N 列の行列 M が以下の条件を満たすとき、"スペシャル行列"と呼ぶことにします。

1 \leq i,j \leq N に対し、i < j のとき M_{i,j}=0 、i \geq j のとき M_{i,j}>0
M_{1,1}=a
長さ N の等比数列 X= ( X_1,X_2, \dots ,X_N ) が存在して、 1 \leq j \leq i \leq N に対し、(M^P) _ {i,j}=M_{i,j} \times X_{i-j+1}
1 \leq k \leq Kに対し、\text{GCD}(M_{A_k,B_k},C_k)=D_k

クエリが Q 個与えられます。 q 番目のクエリではスペシャル行列 M について M_{E_q,F_q} の最小値を 998244353 で割った余りを出力してください。ただし、最小値が存在しない場合は -1 を出力してください。

制約

1 \leq N \leq 1{,}000
2 \leq P \leq 10^{9}
1 \leq a \leq 10^{9}
0 \leq K \leq \min(1{,}000,\frac{N(N-1)}{2})
1 \leq B_k < A_k \leq N
(A_1,B_1),(A_2,B_2), \dots ,(A_K,B_K) はすべて異なる
1 \leq D_k \leq C_k \leq 10^{9}
C_k は D_k で割り切れる
1 \leq Q \leq 70
1 \leq F_q \leq E_q \leq N
入力はすべて整数

小課題

( 1 点) N \leq 30
( 99 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

N P a K
A_1 B_1 C_1 D_1
A_2 B_2 C_2 D_2
\vdots
A_K B_K C_K D_K
Q
E_1 F_1
E_2 F_2
\vdots
E_Q F_Q

出力

Q 行出力してください。q 行目には、q 番目のクエリに対する答えを出力してください。

入力例 1

出力例 1

2
1

1 つめのクエリの場合、例えばM=\begin{pmatrix} 2 & 0 \\ 3 & 2 \end{pmatrix} は M_{2,2} が最小であるスペシャル行列です。

このテストケースは小課題 1 の制約を満たします。

入力例 2

出力例 2

-1

スペシャル行列は存在しません。

このテストケースは小課題 1 の制約を満たします。

P - Score for Cutting Graph

Time Limit: 2 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

各頂点に正整数が書かれた無向グラフ G' に対するスコアを以下で定義します。

G' のすべての連結成分に対して、各連結成分に含まれる頂点に書かれた正整数の総積を求め、その和をスコアとする。

正整数からなる長さ N の数列 A = (A_1, A_2, \ldots, A_N) と正整数 M が与えられます。頂点に 1 から N の番号が付けられた N 頂点 N - 1 辺の単純連結無向グラフ G であって、以下の条件を満たすものが存在するかどうかを判定し、存在するのであれば辺の作成方法を教えてください。

G の頂点 i (1 \leq i \leq N) には A_i が書かれている。
G から 1 本以下の辺を削除して得られる N 個のグラフに対するスコアの総和が M 以下となる。

T 個のテストケースが与えられるので、それぞれについて答えを求めてください。

制約

1 \leq T \leq 5
2 \leq N \leq 200{,}000
1 \leq M \leq 10^{18}
1 \leq A_i \leq 10^{18}
1 つの入力に含まれるテストケースについて、N の総和は 200{,}000 以下
入力はすべて整数

小課題

(1 点) N \leq 7
(99 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

T
\mathrm{case}_1
\vdots
\mathrm{case}_T

各テストケースは以下の形式で与えられます。

N M
A_1 A_2 \ldots A_N

出力

k 番目に \mathrm{case}_k の答えを出力してください。スコアの総和を M 以下にすることが不可能である場合は No と出力してください。可能である場合は 1 行目に Yes と出力し、2 行目以降に G の辺の作成方法を以下の形式に従って N-1 行出力してください。

s_1 t_1
s_2 t_2
\vdots
s_{N-1} t_{N-1}

s_j, t_j は G の辺を表します。これは頂点 s_j と頂点 t_j を結ぶ辺であることを示します。

答えが複数存在する場合、どれを出力しても正解となります。

入力例 1

3
4 60
1 2 3 4
4 24
1 2 3 4
7 1000000000000000000
1 2 3 4 5 6 7

出力例 1

1 つ目のテストケースとその出力例について、例えば以下のような場合が考えられます。

どの辺も削除されない場合、スコアは (1 \times 2 \times 3 \times 4) = 24
1 番目の辺が削除される場合、スコアは (2) + (1 \times 3 \times 4) = 14
2 番目の辺が削除される場合、スコアは (3) + (1 \times 2 \times 4) = 11
3 番目の辺が削除される場合、スコアは (4) + (1 \times 2 \times 3) = 10

スコアの総和は 59 となります。他にもスコアの総和が 60 以下となる G はありますが、そのどれを出力しても正解となります。

2 つ目のテストケースについて、スコアの総和が 24 以下になるような G は存在しないため、No を出力します。

このケースは小課題 1 の制約を満たします。

入力例 2

3
10 20
1 1 1 1 1 1 1 1 1 1
4 3000
20 24 1 6
10 3000000
20 2 4 1 6 20 2 4 1 6

出力例 2

このケースは小課題 1 の制約を満たしません。

Q - Kurukuru

Time Limit: 2 sec / Memory Limit: 1024 MB

配点 : 100 点

問題文

この問題では以下の数式表現を用います。

(i,j) : 2 次元配列の上から i+1 行目、左から j+1 列目の場所
A_{i,j} : 2 次元配列 A の上から i+1 行目、左から j+1 列目の値
p \bmod q : 非負の整数 p を正の整数 q で割った余り

N \times N の 2 次元配列に対する M 個の操作が与えられます。各操作は整数 t といくつかの整数で表され、t の値に応じて、(i,j) (0 \leq i,j < N) に対して以下の操作を同時に行います。

t = 1 のとき、(i, j) にある数値を ((i x + a) \bmod N, (j y + b) \bmod N) に移動させる。ただし x と N、 y と N はどちらも互いに素であることが保証され、したがって各数値の移動先は重複しない。
t = 2 のとき、(i, j) にある数値を (j, i) に移動させる。

Q 個のクエリが与えられます。各クエリは L,R,c,d,e,f の 6 つの整数からなります。それぞれ A_{i,j} = i N + j である N \times N の 2 次元配列 A に対して L, L + 1, \dots , R 番目の操作を順番に行い、操作後の 2 次元配列 A' について \sum\limits_{i = c}^{d} \sum\limits_{j=e}^{f} A_{i, j}' を 998244353 で割った余りを求めてください。

制約

2 \leq N \leq 10^{9}
1 \leq M \leq 200{,}000
1 \leq Q \leq 200{,}000
1 \leq x < N
1 \leq y < N
x と N, y と N は互いに素
0 \leq a < N
0 \leq b < N
1 \leq L \leq R \leq M
0 \leq c \leq d < N
0 \leq e \leq f < N
入力はすべて整数

小課題

(1 点) N\leq 10
(99 点) 追加の制約はない

入力

入力は以下の形式で標準入力から与えられます。

N M Q
\mathrm{Operation}_1
\mathrm{Operation}_2
\vdots
\mathrm{Operation}_M
\mathrm{Query}_1
\mathrm{Query}_2
\vdots
\mathrm{Query}_Q

各操作 (\mathrm{Operation}) は以下に示す 2 つの形式のいずれかです。

1 x y a b

各クエリ (\mathrm{Query}) は以下の形式です。

L R c d e f

出力

Q 行出力してください。 i 行目には、 i 番目のクエリに対する答えを出力してください。

入力例 1

3 5 2
1 1 1 2 1
1 2 1 0 2
2
1 1 2 1 0
2
2 3 0 1 1 2
1 5 0 2 0 2

出力例 1

24
36

1 番目のクエリでは、2 番目から 3 番目までの操作を適用します。操作前の 2 次元配列は A=\begin{pmatrix} 0 & 1 & 2 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{pmatrix} です。 2 番目の操作を適用すると、\begin{pmatrix} 1 & 2 & 0 \\ 7 & 8 & 6 \\ 4 & 5 & 3 \end{pmatrix} となります。さらに 3 番目の操作を適用すると、\begin{pmatrix} 1 & 7 & 4 \\ 2 & 8 & 5 \\ 0 & 6 & 3 \end{pmatrix} となります。 A' = \begin{pmatrix} 1 & 7 & 4 \\ 2 & 8 & 5 \\ 0 & 6 & 3 \end{pmatrix} としたとき、 \sum\limits_{i=0}^1 \sum\limits_{j=1}^2 A'_{i,j} = 7+4+8+5 = 24 です。

2 番目のクエリは、 1 番目から 5 番目までの操作を適用します。すべての操作を適用した後、A' = \begin{pmatrix} 5 & 3 & 4 \\ 8 & 6 & 7 \\ 2 & 0 & 1 \end{pmatrix} となりますが、当然そのすべての要素の和は操作前に等しく 36 です。

このテストケースは小課題 1 の制約を満たします。

入力例 2

999999937 8 3
1 314159265 358979323 846264338 327950288
1 419716939 937510582 97494459 230781640
2
1 628620899 862803482 534211706 798214808
1 651328230 664709384 460955058 223172535
1 940812848 111745028 410270193 852110555
2
1 964462294 895493038 196442881 97566593
3 3 344612847 564823378 67831652 712019091
3 7 45648566 923460348 610454326 648213393
1 8 60726024 914127372 458700660 631558817

出力例 2

511746849
453803153
685820807

このテストケースは小課題 1 の制約を満たしません。