D - さんかく
Editorial
 /
/ 
平面上に存在する N(N は 3 の倍数)個の点を用いて三角形を N/3 個作り、その面積の合計値を出来るだけ大きくするゲームがあります。
ただし、i(0≦i≦N-1)番目の点を示す X 座標の値 x_i と Y 座標の値 y_i はそれぞれ 0≦x_i≦100,000 と 0≦y_i≦100,000 を満たします。
高橋君はこのゲームをコンピュータを使って挑戦します。
しかし、彼は良いアルゴリズムが思いつかなかったため、ランダムで解くことにしました。
高橋君はランダムに 3 つずつ点を選び、N/3 個の三角形を作ります。
これを 1,000 万回行い、最も良かった答えを採用します。
貴方は、高橋君の解答と同じか、それよりより値が大きくなる解答を作りたいです。
そのような三角形の組み合わせを出力してください。
入力は以下の形式で標準入力から与えられる。
テストデータには以下に示す 4 種類のデータセットのいずれかが含まれており、それぞれ与えられる点の数である N の値が異なっている。
あるデータセットに対して、高橋君が選択した三角形の面積の合計値と等しい、もしくは大きい解答を出力できたとき、あなたはそのデータセットに対して 2 点を得ることができる。
三角形の面積の合計値が高橋君の解答と同じか、もしくはそれより大きい解答となる三角形の組み合わせを、頂点となる番号で出力せよ。
各三角形の頂点となる番号を 1 行につき 1 つの三角形が構成されるように出力し、半角スペースで区切ること。
また各三角形を出力する順番、および 1 つの三角形における頂点の出力の順番は問わない。
なお、行の終端には改行が必要である。

 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
問題文
ただし、i(0≦i≦N-1)番目の点を示す X 座標の値 x_i と Y 座標の値 y_i はそれぞれ 0≦x_i≦100,000 と 0≦y_i≦100,000 を満たします。
高橋君はこのゲームをコンピュータを使って挑戦します。
しかし、彼は良いアルゴリズムが思いつかなかったため、ランダムで解くことにしました。
高橋君はランダムに 3 つずつ点を選び、N/3 個の三角形を作ります。
これを 1,000 万回行い、最も良かった答えを採用します。
貴方は、高橋君の解答と同じか、それよりより値が大きくなる解答を作りたいです。
そのような三角形の組み合わせを出力してください。
入力
N
x_0 y_0
:
:
x_{N-1} y_{N-1}
- 入力は N+1 行ある。
- 1 行目には平面上の点の個数を表す整数 N\ (3≦N≦3,000) が与えられる。ただし、N は 3 の倍数である。
- 2 行目から N+1 行目までの N 行は点の座標を示している。
- i\ (0≦i≦N-1) 番目に与えられる座標 (x_i, y_i) は 0≦x_i≦100,000 かつ 0≦y_i≦100,000 の範囲でランダムに与えられる。
- 0≦i≦N-1 と 0≦j≦N-1 を満たし、i≠j である 2 つの整数 i と j において、x_i≠x_j もしくは y_i≠y_j の少なくとも片方を満たすことが保証されている。
部分点
あるデータセットに対して、高橋君が選択した三角形の面積の合計値と等しい、もしくは大きい解答を出力できたとき、あなたはそのデータセットに対して 2 点を得ることができる。
- level1 (各 2 点、10 個): N=9
- level2 (各 2 点、10 個): N=18
- level3 (各 2 点、15 個): N=300
- level4 (各 2 点、15 個): N=3,000
出力
各三角形の頂点となる番号を 1 行につき 1 つの三角形が構成されるように出力し、半角スペースで区切ること。
また各三角形を出力する順番、および 1 つの三角形における頂点の出力の順番は問わない。
なお、行の終端には改行が必要である。
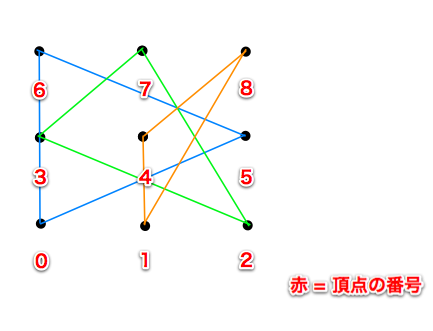
入力例 1
9 0 0 1 0 2 0 0 1 1 1 2 1 0 2 1 2 2 2
出力例 1
3 7 2 4 8 1 6 0 5

- 入力例 1 を図示すると、上図のようになります。

- 入力例 1 に対して、高橋君のアルゴリズムでは、上図のように点を選択します。この例と同じ面積、もしくは面積の合計が大きい回答を出力してください。
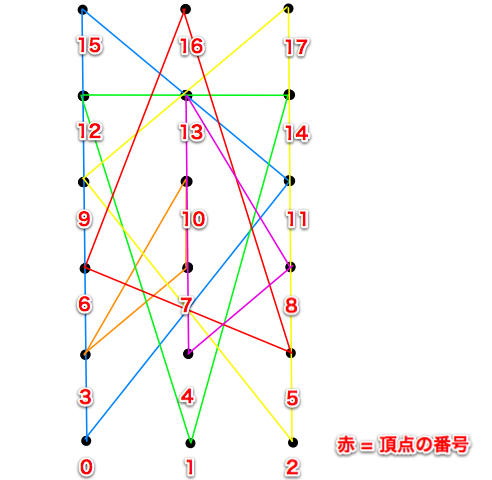
入力例 2
18 0 0 1 0 2 0 0 1 1 1 2 1 0 2 1 2 2 2 0 3 1 3 2 3 0 4 1 4 2 4 0 5 1 5 2 5
出力例 2
11 0 15 3 7 10 6 16 5 2 17 9 12 14 1 8 13 4

- 入力例 2 に対して、高橋君のアルゴリズムでは、上図のように点を選択します。この例と同じ面積、もしくは面積の合計が大きい回答を出力してください。