 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
問題文
マス目からなる迷路があります。
迷路の各マスは、巣、角砂糖、壁、空き地のいずれかであり、アリ達は左上にある巣のマスから右下にある角砂糖のあるマスまで行きたいと思っています。
角砂糖のあるマスを含む、壁以外の任意の地点へは到達することができ、またループになっている経路はありません。
加えて、(奇数,奇数) の地点は必ず壁であり、(偶数,偶数) の地点は必ず空き地です。
ここでの座標は、左上の巣のある地点を (0,0) とし、1 つ右の座標は (1,0)、1 つ下の座標は (0,1) になります。
このような迷路の例を図 1 に示します。
黄緑色の部分が (奇数,奇数) の地点、橙色の部分が (偶数,偶数) の地点になります。
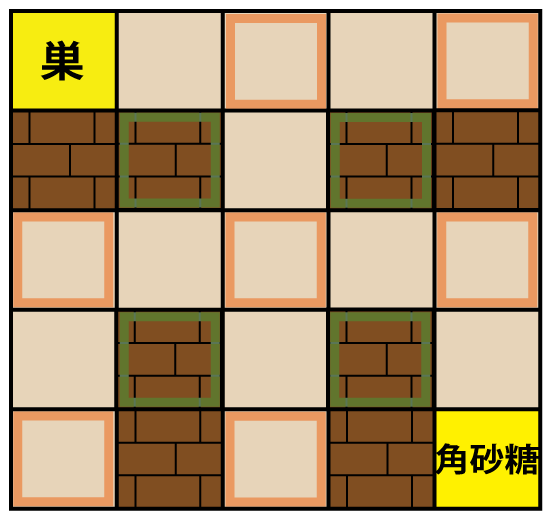
ここでのアリは、直進できる場合は直進し、壁にぶつかった場合は 1/2 の確率で左、1/2 の確率で右に曲がる性質を持っています。壁にぶつかっても左右のいずれかに壁がある場合は、その反対方向に必ず曲がります。
どちらにも曲がれないような場合(三方向が壁または迷路外になった場合)は、その場でアリは死亡してしまい壁になります。
なお、巣のマスの下は壁になっているので、最初は右方向にしか進めません。また、角砂糖のあるマスの左は壁になっているので、上方向からしか角砂糖のあるマスに到達できません。
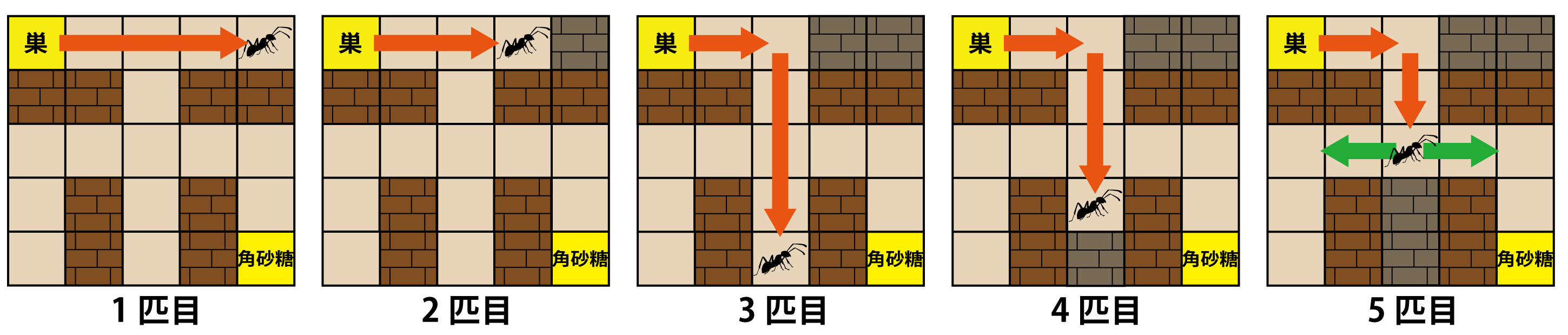
例えば図 1 の場合を図 2 に示すと、1 匹目のアリは直進するので右上の地点 (4,0) で壁と迷路外に囲まれて死亡してしまいます。
2 匹目のアリは (4,0) が 1 匹目のアリにより壁になっているので、その 1 つ手前の (3,0) で死亡し壁になります。
その結果、3 匹目、4 匹目のアリは (2,0) で右に曲がり、(2,4)、(2,3) でそれぞれ死亡します。
5 匹目のアリは (2,2) で直進できないので、(1,2) または (3,2) に進みます。
(1,2) の方向に進んだ場合は (0,4) で死亡しますが、(3,2) の方向に進んだ場合は角砂糖へと到達できます。
アリが角砂糖にに辿り着くまでこのような行動を繰り返したとすると、辿り着くまでに必要なアリの数の期待値を求めなさい。
入力
N
c_{(0,0)}c_{(1,0)}‥‥c_{(N-1,0)}
c_{(1,1)}c_{(1,1)}‥‥c_{(N-1,1)}
:
:
c_{(0,N-2)}c_{(1,N-2)}‥‥c_{(N-1,N-2)}
c_{(0,N-1)}c_{(1,N-1)}‥‥c_{(N-1,N-1)}
- 入力は N+1 行ある。
- 1 行目には、与えられる迷路の縦と横の長さを表す整数 N(5≦N≦49) が与えられる。
- N は奇数である。
- 2 行目からの N 行には、各行に図の形を表す状態 c_{(i,j)}(0≦i,j≦N-1) が N 文字与えられる。
- c_{(i,j)} は下記のいずれかであり、それぞれ地点 (i,j) のマスが下記のような状態であることを表す。
S: そのマスが巣であることを表す。G: そのマスに角砂糖があることを表す。#: そのマスが壁であることを表す。.: そのマスが空き地であることを表す。
- c_{(0,0)} は必ず
Sであり、c_{(N-1,N-1)} は必ずGである。また、SとGは、それぞれこの場所にしか存在しない。 Sから 1 つ下の地点 c_{(1,0)} とGから 1 つ左の地点 c_{(N-1,N-2)} は必ず#である。- i と j が共に奇数の地点は必ず
#であり、i と j が共に偶数の地点は必ず.である。
- c_{(i,j)} は下記のいずれかであり、それぞれ地点 (i,j) のマスが下記のような状態であることを表す。
部分点
出力
誤差は絶対誤差あるいは相対誤差の少なくとも片方が 1e−6(10^{-6}) 以下であれば許容する。 なお、行の終端には改行が必要である。
入力例 1
5 S.... ##.## ..... .#.#. .#.#G
出力例 1
5.937500000
- それぞれの匹数で角砂糖まで到達できる確率を求めると、以下のようになる。
- 5 匹で到達できる確率:1/2
- 6 匹で到達できる確率:1/2×1/2
- (2,2) の分岐で 5 匹目は (1,2) の方向へ、6 匹目は (3,2) の方向へ曲がった場合
- 7 匹で到達できる確率:1/2^3
- 8 匹で到達できる確率:1/2^4
- 9 匹で到達できる確率:1/2^4×1
- したがって、5×1/2+6×1/2×1/2+7×1/2^3+8×1/2^4+9×1/2^4×1=5.9375 となる。
入力例 2
9 S........ ####.#### ......... .#####.## ...#.#... .#.#.#### .#...#... .#.#.#.#. .#.#...#G
出力例 2
18.029407501
入力例 3
13 S............ ####.#.#.#### .....#.#...#. .###########. .....#.#..... .#.###.###.## .#...#.#..... ##.#.#.#####. .#.#.....#... .#.###.#.#.## ...#...#..... .#.#.#.#.###. .#.#.#.#...#G
出力例 3
35.000000000