 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 400 点
問題文
2 \times N のマス目があります. すぬけ君は,このマス目に N 個のドミノを,重ならないように敷き詰めました. ここで,ドミノは,1 \times 2 または 2 \times 1 のマス目を覆うことができます.
すぬけ君は,赤色,水色,緑色の 3 色を使って,これらのドミノを塗ることにしました. このとき,辺で接しているドミノは異なる色で塗るようにします. ここで,必ずしも 3 色すべてを使う必要はありません.
このような塗り方が何通りあるかを mod 1000000007 で求めてください.
ただし,ドミノの敷き詰め方は,文字列 S_1, S_2 を用いて,次のようにして与えられます.
- 各ドミノは,それぞれ異なる英小文字または英大文字で表される.
- S_i の j 文字目は,マス目の上から i 番目,左から j 番目のマスにどのドミノがあるかを表す.
制約
- 1 \leq N \leq 52
- |S_1| = |S_2| = N
- S_1, S_2 は英小文字または英大文字からなる
- S_1, S_2 は正しいドミノの敷き詰め方を表している
入力
入力は以下の形式で標準入力から与えられる。
N S_1 S_2
出力
ドミノを塗る方法の数を mod 1000000007 で出力せよ.
入力例 1
3 aab ccb
出力例 1
6
次の 6 通りあります.
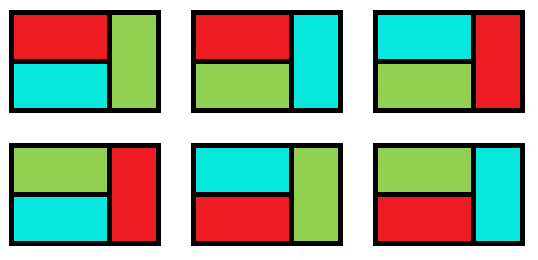
入力例 2
1 Z Z
出力例 2
3
必ずしもすべての色を使わなくてもよいことに注意してください.
入力例 3
52 RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn
出力例 3
958681902
Score : 400 points
Problem Statement
We have a board with a 2 \times N grid. Snuke covered the board with N dominoes without overlaps. Here, a domino can cover a 1 \times 2 or 2 \times 1 square.
Then, Snuke decided to paint these dominoes using three colors: red, cyan and green. Two dominoes that are adjacent by side should be painted by different colors. Here, it is not always necessary to use all three colors.
Find the number of such ways to paint the dominoes, modulo 1000000007.
The arrangement of the dominoes is given to you as two strings S_1 and S_2 in the following manner:
- Each domino is represented by a different English letter (lowercase or uppercase).
- The j-th character in S_i represents the domino that occupies the square at the i-th row from the top and j-th column from the left.
Constraints
- 1 \leq N \leq 52
- |S_1| = |S_2| = N
- S_1 and S_2 consist of lowercase and uppercase English letters.
- S_1 and S_2 represent a valid arrangement of dominoes.
Input
Input is given from Standard Input in the following format:
N S_1 S_2
Output
Print the number of such ways to paint the dominoes, modulo 1000000007.
Sample Input 1
3 aab ccb
Sample Output 1
6
There are six ways as shown below:

Sample Input 2
1 Z Z
Sample Output 2
3
Note that it is not always necessary to use all the colors.
Sample Input 3
52 RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn
Sample Output 3
958681902