Consider the harvesting from the \(i\)-th tree on the \(D_i\)-th day. If the last harvesting from the \(i\)-th tree was on the \(B_i\)-th day, then \(i \cdot (D_q- B_i)\) fruits is collected from the \(i\)-th tree in this harvesting. Therefore, we can consider the following naive solution for this problem:

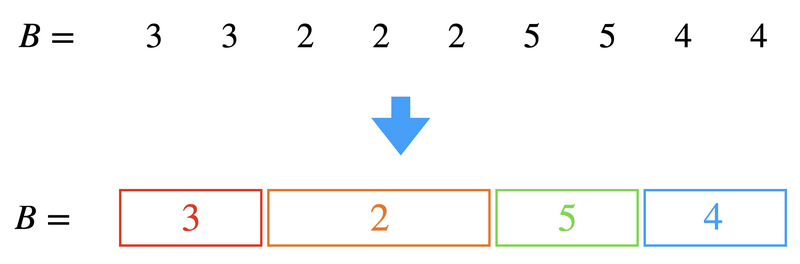
• First, prepare an array \(B\) of length \(N\) to store for each \(i = 1, 2, \ldots, N\) the last day \(B[i]\) on which a harvesting was done on tree \(i\). For convenience, we initialize them by \(B[1] = B[2] = \cdots = B[N] = 0\).

• Then, for each \(q = 1, 2, \ldots, Q\), do the following:

  • Print the sum of fruits \(\sum_{i = L_q}^{R_q} i \cdot (D_q - B[i])\) collected in the \(q\)-th harvesting.
  • For each \(i = L_q, L_q+1, \ldots, R_q\), update \(B[i] \leftarrow D_q\).

This way, the worst time complexity is \(\mathrm{\Theta}(NQ)\), so it is hopeless that this works in the execution time limit. Instead, we will describe a better way: split \(B\) into blocks so that each block has the same value, and harvest fruits from each block at once.

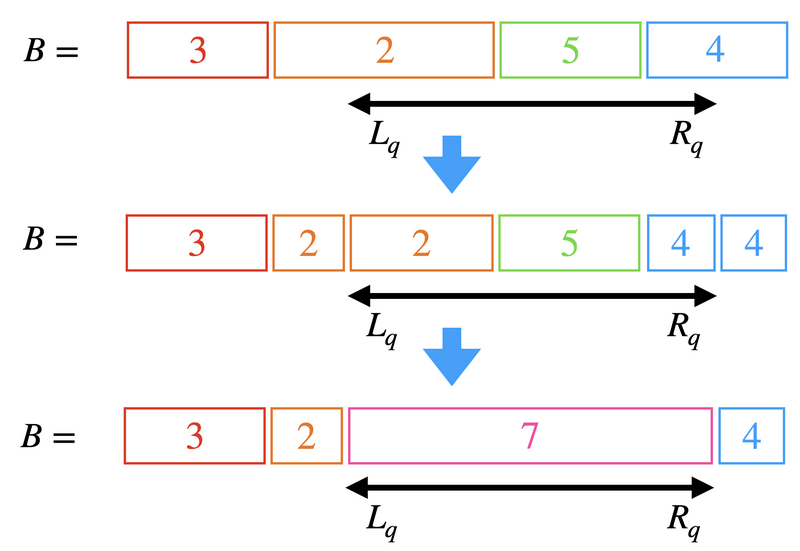
Initially, we only have a block \([1, N]\) of value \(0\). For each harvesting, we update the blocks as follows. (We assume that every block is either completely included in or disjoint from the harvesting segment, which can be accomplished by dividing block striding the ends of the segment, as from the first to the second step in the figure below.)

• For each block \([l, r]\) included in the harvesting segment \([L_q, R_q]\), find the total number of fruits collected from the tree in that block as \(\sum_{i = l}^{r} i \cdot (D_q - B[i]) = (D_q - d) (l+r) (r-l+1) / 2\) (where \(d\) denotes the value of the block), and print their sum.
• Remove all blocks included in the harvesting segment \([L_q, R_q]\), adding a single block \([L_q, R_q]\) of value \(D_q\) instead (as in the second to the third step in the figure below).

Since exactly one block \([L_q, R_q]\) is added by each harvesting, the blocks are inserted \(\mathrm{O}(Q)\) times in the entire algorithm. Once harvested, the block is removed, so the number of times a block is removed does not exceed the number of times a block is added, which is \(\mathrm{O}(Q)\) as well. By managing blocks by a balanced binary tree, we can add and remove a block in an \(\mathrm{O}(\log Q)\) time, the problem can be solved by the algorithm above in a total of \(\mathrm{O}(Q \log Q)\) time.