In the definition of the frustration, we call \(A_i\) and \(B_i\) the coefficient and \(|x-y|\) the bias. (So, the frustration is the product of the coefficient and bias.)

1. The structure of the optimal solution

In fact, the optimal solution is always in the form illustrated in the figure below. (The case where \(N\) is even and \(M\) is odd is equivalent to \(N\) is odd and \(M\) is even, so we ignore it.)

Explanation of the figure: a red circle denotes a dog, a blue one denotes a cat, and a white one denotes a dog or a cat. An arrow over a subarray of the circles means that the coefficient is sorted in ascending order in the direction of the arrow. For example, the topmost figure expresses the concatenation of “\(\frac{N-1}{2}\) dogs and \(\frac{M-1}{2}\) cats arranged in ascending order of the coefficients”, “the dog with maximum \(A_i\)”, “the dog with minimum \(B_i\)”, and “\(\frac{N-1}{2}\) dogs and \(\frac{M-1}{2}\) cats arranged in descending order of the coefficients”.

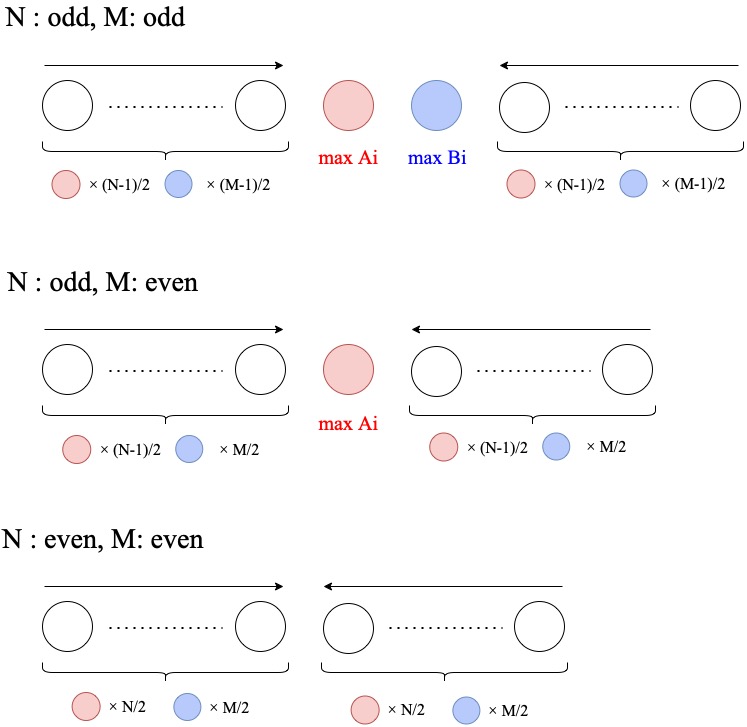
We prove the optimality for each pattern.

Click here to skip the proof

If \(N\) and \(M\) are both odd

We divide the property to prove into three parts.

1. The central dog (the \(\frac{N+1}{2}\)-th dog from the left) and the central cat (the \(\frac{M+1}{2}\)-th cat from the left) are adjacent.
2. The central dog and cat has the maximum coefficient among that kind of animal.
3. For the animals in the left and right of the central animals, the animals closer to the center always has larger coefficient.

1. The central dog and cat are adjacent.

If there is another animal between the central dog and cat,

Move the dogs in between to the next to the central cat, and the cats in between to the next to the central dogs. No animal gains bias, so the solution does not get worse. Thus, we may assume that the central dog and cat are adjacent in the optimal solution.

2. The central dog and cat has the maximum coefficient among that kind of animal.

If the central dog and cat are adjacent, their biass are both \(1\), which is the minimum bias, so it is optimal to assign those with the maximum coefficient (permutation inequality).

3. For the animals in the left and right of the central animals, the animals closer to the center always has larger coefficient.

Suppose that there are two animals adjacent in a sequence, where the animal closer to the center has smaller coefficient than the further one. If you swap these two animals,

• if the two are both dogs or both cats, the bias does not change, so the frustrations are invariant too.
• if one of them is a dog and the other is a cat, then the bias of the one closer to the center increases by \(2\), and the other bias decreases by \(2\). By the assumption of the order of the coefficient, the sum of the frustrations decreases.

Therefore, we may repeatedly swap adjacent pair of animals with illegal order of coefficients to arrange them so that “the animals closer to the center always has larger coefficient” without worsening the solution.

If \(N\) is odd and \(M\) is even

If the central dog is not between the \(\frac{M}{2}\)-th and \((\frac{M}{2}+1)\)-th cat from the left,

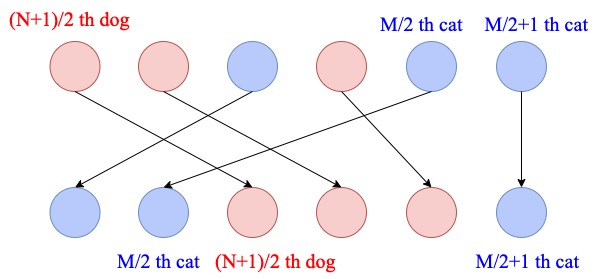
this operation does not change the solution. Now it is equivalent to the case where \(N\) and \(M\) are both od.

If \(N\) and \(M\) are both even

Similarly, consider the following operation.

Considering the \(\frac{N}{2}\)-th dog, \((\frac{N}{2}+1)\)-th dog, \(\frac{M}{2}\)-th cat, and \((\frac{M}{2}+1)\)-th cat from the left, the operation above gets rid of “dog-dog-cat-cat” and “cat-cat-dog-dog” patterns, leaving out four choices: “dog-cat-dog-cat”, “cat-dog-cat-dog”, “dog-cat-cat-dog”, or “cat-dog-dog-cat.” In any case, the \(\frac{N+M}{2}\) animals in the left consist of \(\frac{N}{2}\) dogs and \(\frac{M}{2}\), so the same discussion as 3. can be applied to the left and right half.

2. Evaluation

If \(N\) or \(M\) is odd, we can place an appropriate central animal to boil down to the case where \(N\) and \(M\) are both even.

Now we assume that \(N\) and \(M\) are even. As already described, only the following sequence should be considered:

• concatenation of \(P\) and “reverse of \(Q\)”, where \(P\) and \(Q\) are sequences consisting of \(\frac{N}{2}\) dogs and \(\frac{M}{2}\) cats in ascending order of the frustration (so that each animal appears exactly once in either \(P\) or \(Q\)).

Therefore, it is sufficient to do a Dynamic Programming (DP) where the animals are inspected in ascending order of the coefficients while being appended to \(P\) or \(Q\).

Specifically,let

\[\mathrm{dp}[i][j][k] = \text{The minimum possible sum of frustrations resulting from placing }i\text{ animals, where }P\text{ contains }j\text{ dogs and }k\text{ cats},\]

then the bias of a new animal can be computed from \(i, j\), and \(k\), which can be evaluated in an \(O(1)\) time. The sought value is \(\mathrm{dp}[N+M][\frac{N}{2}][\frac{M}{2}]\).

The time complexity is \(O(NM(N+M))\).

Bonus: someone found an \(O((N+M)\log (N+M ))\) solution (tatyam’s conjecture (Japanese)、noshi’s proof (Japanese)).

Sample code (C++):

#include<bits/stdc++.h>

using namespace std;

using ll = long long;

void chmin(ll &a, ll b) {
    a = min(a, b);
}

int main() {
    int n, m;
    cin >> n >> m;
    vector<int> a(n), b(m);
    for (int &i: a) cin >> i;
    for (int &i: b) cin >> i;
    sort(a.begin(), a.end());
    sort(b.begin(), b.end());
    ll ans = 0;
    if (n & 1) {
        if (m & 1) ans += a.back();
        ans += accumulate(b.begin(), b.end(), 0LL);
        a.pop_back();
        --n;
    }
    if (m & 1) {
        ans += accumulate(a.begin(), a.end(), 0LL);
        b.pop_back();
        --m;
    }
    // pair の第 1 引数 : A_i または B_i
    //        第 2 引数 : 犬ならば 0、猫ならば 1
    vector<pair<int, int>> v;
    for (int i = 0; i < n; i++) v.emplace_back(a[i], 0);
    for (int i = 0; i < m; i++) v.emplace_back(b[i], 1);
    sort(v.begin(), v.end());
    
    vector dp(n + m + 1, vector(n + 1, vector<ll>(m + 1, 1LL << 60)));
    dp[0][0][0] = 0;
    int dog = 0, cat = 0;
    for (int i = 0; i < n + m; i++) {
        ll now = v[i].first;
        if (v[i].second == 0) {
            for (int j = 0; j <= dog; j++) {
                for (int k = 0; k <= cat; k++) {
                    chmin(dp[i + 1][j + 1][k], dp[i][j][k] + now * (m - k * 2));
                    chmin(dp[i + 1][j][k], dp[i][j][k] + now * (m - (cat - k) * 2));
                }
            }
            ++dog;
        } else {
            for (int j = 0; j <= dog; j++) {
                for (int k = 0; k <= cat; k++) {
                    chmin(dp[i + 1][j][k + 1], dp[i][j][k] + now * (n - j * 2));
                    chmin(dp[i + 1][j][k], dp[i][j][k] + now * (n - (dog - j) * 2));
                }
            }
            ++cat;
        }
    }
    ans += dp[n + m][n / 2][m / 2];
    cout << ans << endl;
}