C - Tree Restoring

Contest Duration: 2016-10-01(Sat) 12:00 - 2016-10-01(Sat) 13:50 (local time) (110 minutes) Back to Home

C - Tree Restoring Editorial

Time Limit: 2 sec / Memory Limit: 256 MB

配点 : $700$ 点

問題文

青木君は数列と木が大好きです。

青木君はある日高橋くんから長さ $N$ の数列 $a_1, a_2, ..., a_N$ を貰いました。そしてこの数列を見て、木を作りたくなりました。

青木君が作りたいのは、頂点数が $N$ で、全ての $i = 1,2,...,N$ について頂点 $i$ と最も遠い頂点の距離が $a_i$ となる木です。なお、辺の長さは全て $1$ とします。

これを満たす木が存在するか判定してください。

制約

$2 ≦ N ≦ 100$
$1 ≦ a_i ≦ N-1$

入力

入力は以下の形式で標準入力から与えられる。

 $N$ 
 $a_1$   $a_2$   $...$   $a_N$

出力

条件を満たす木が存在するならば Possible、しないならば Impossible と出力する。

入力例 1Copy

Copy

5
3 2 2 3 3

出力例 1Copy

Copy

Possible

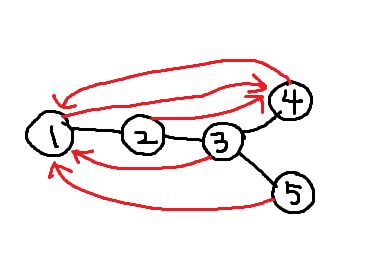
上図は条件を見たす木の一例です。赤い矢印は最も遠い頂点への経路を表します。

入力例 2Copy

Copy

3
1 1 2

出力例 2Copy

Copy

Impossible

入力例 3Copy

Copy

10
1 2 2 2 2 2 2 2 2 2

出力例 3Copy

Copy

Possible

入力例 4Copy

Copy

10
1 1 2 2 2 2 2 2 2 2

出力例 4Copy

Copy

Impossible

入力例 5Copy

Copy

6
1 1 1 1 1 5

出力例 5Copy

Copy

Impossible

入力例 6Copy

Copy

5
4 3 2 3 4

出力例 6Copy

Copy

Possible

Score : $700$ points

Problem Statement

Aoki loves numerical sequences and trees.

One day, Takahashi gave him an integer sequence of length $N$ , $a_1, a_2, ..., a_N$ , which made him want to construct a tree.

Aoki wants to construct a tree with $N$ vertices numbered $1$ through $N$ , such that for each $i = 1,2,...,N$ , the distance between vertex $i$ and the farthest vertex from it is $a_i$ , assuming that the length of each edge is $1$ .

Determine whether such a tree exists.

Constraints

$2 ≦ N ≦ 100$
$1 ≦ a_i ≦ N-1$

Input

The input is given from Standard Input in the following format:

 $N$ 
 $a_1$   $a_2$   $...$   $a_N$

Output

If there exists a tree that satisfies the condition, print Possible. Otherwise, print Impossible.

Sample Input 1Copy

Copy

5
3 2 2 3 3

Sample Output 1Copy

Copy

Possible

The diagram above shows an example of a tree that satisfies the conditions. The red arrows show paths from each vertex to the farthest vertex from it.

Sample Input 2Copy

Copy

3
1 1 2

Sample Output 2Copy

Copy

Impossible

Sample Input 3Copy

Copy

10
1 2 2 2 2 2 2 2 2 2

Sample Output 3Copy

Copy

Possible

Sample Input 4Copy

Copy

10
1 1 2 2 2 2 2 2 2 2

Sample Output 4Copy

Copy

Impossible

Sample Input 5Copy

Copy

6
1 1 1 1 1 5

Sample Output 5Copy

Copy

Impossible

Sample Input 6Copy

Copy

5
4 3 2 3 4

Sample Output 6Copy

Copy

Possible