 /
/ 
Time Limit: 4 sec / Memory Limit: 256 MB
配点 : 1600 点
問題文
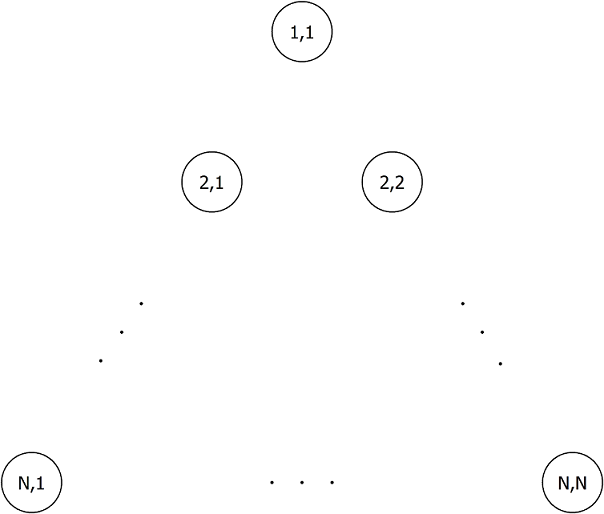
下図のように,1 辺が N 個の点からなる正三角形状に,N(N+1)/2 個の点が並んでいます. 上から i 段目の左から j 番目の点を (i, j) で表すことにします(1 \leq i \leq N, 1 \leq j \leq i). また,(i+1, j) を (i, j) のすぐ左下の点,(i+1, j+1) を (i, j) のすぐ右下の点と呼ぶことにします.
高橋君は,この点を結んで,M 個の折れ線 1, 2, ..., M を描くことにしました. 各折れ線は,(1, 1) から始めて,「現在いる点のすぐ左下の点かすぐ右下の点を選び,現在いる点と選んだ点を直線で結んだのち,選んだ点へ移動する」 ことを N-1 回繰り返すことで得られます. すなわち,ある X_{i,1}, ..., X_{i,N} が存在して,次が成り立ちます:
- 折れ線 i は,N 個の点 (1, X_{i,1}), (2, X_{i,2}), ..., (N, X_{i,N}) をこの順で結んでいる.
- j=1, 2, ..., N-1 に対して,X_{i,j+1} = X_{i,j} または X_{i,j+1} = X_{i,j}+1 が成り立つ.
高橋君は,折れ線 i+1 が折れ線 i の左に来ることはないように折れ線を描きたいです. つまり,j=1, 2, ..., N に対して,X_{1,j} \leq X_{2,j} \leq ... \leq X_{M,j} が成り立ちます.
また,高橋君は,折れ線の曲がり方について K 個の条件を満たすように折れ線を描かなければなりません. i 番目の条件は (A_i, B_i, C_i) で表され,これは次を意味します:
- C_i=0 のときは,折れ線 A_i を描くとき,B_i 回目の移動においては,その時いる点のすぐ左下の点を選ぶ.
- C_i=1 のときは,折れ線 A_i を描くとき,B_i 回目の移動においては,その時いる点のすぐ右下の点を選ぶ.
すなわち,X_{A_i, {B_i}+1} = X_{A_i, B_i} + C_i を意味します.
高橋君が M 個の折れ線を描く方法が何通りあるかを mod 1000000007 で求めてください.
注意
提出を行う前に,「コードテスト」を利用して実行時間を計測することを強く推奨する.
制約
- 1 \leq N \leq 20
- 1 \leq M \leq 20
- 0 \leq K \leq (N-1)M
- 1 \leq A_i \leq M
- 1 \leq B_i \leq N-1
- C_i = 0,1
- (A_i, B_i) として同じ組は複数回与えられない.
入力
入力は以下の形式で標準入力から与えられる。
N M K A_1 B_1 C_1 A_2 B_2 C_2 : A_K B_K C_K
出力
高橋君が M 個の折れ線を描く方法は何通りあるかを mod 1000000007 で出力せよ.
入力例 1
3 2 1 1 2 0
出力例 1
6
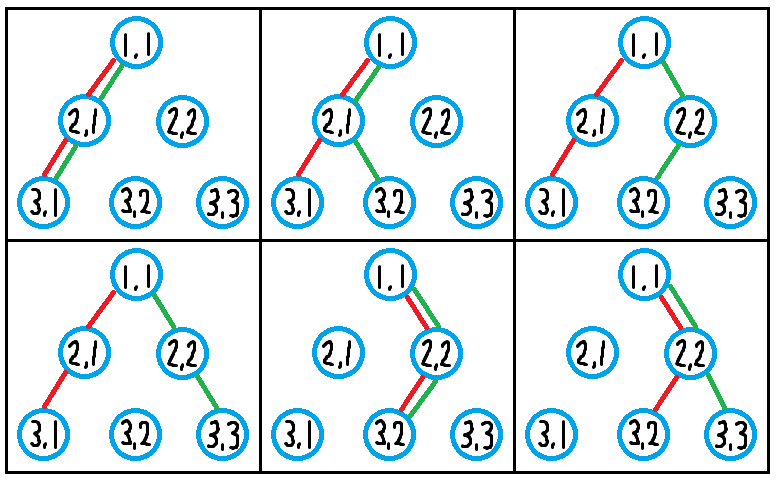
下図に示すように,6 通りの描き方があります.ただし,赤線は折れ線 1,緑線は折れ線 2 を表します:
入力例 2
3 2 2 1 1 1 2 1 0
出力例 2
0
入力例 3
5 4 2 1 3 1 4 2 0
出力例 3
172
入力例 4
20 20 0
出力例 4
881396682
Score : 1600 points
Problem Statement
There are N(N+1)/2 dots arranged to form an equilateral triangle whose sides consist of N dots, as shown below. The j-th dot from the left in the i-th row from the top is denoted by (i, j) (1 \leq i \leq N, 1 \leq j \leq i). Also, we will call (i+1, j) immediately lower-left to (i, j), and (i+1, j+1) immediately lower-right to (i, j).

Takahashi is drawing M polygonal lines L_1, L_2, ..., L_M by connecting these dots. Each L_i starts at (1, 1), and visits the dot that is immediately lower-left or lower-right to the current dots N-1 times. More formally, there exist X_{i,1}, ..., X_{i,N} such that:
- L_i connects the N points (1, X_{i,1}), (2, X_{i,2}), ..., (N, X_{i,N}), in this order.
- For each j=1, 2, ..., N-1, either X_{i,j+1} = X_{i,j} or X_{i,j+1} = X_{i,j}+1 holds.
Takahashi would like to draw these lines so that no part of L_{i+1} is to the left of L_{i}. That is, for each j=1, 2, ..., N, X_{1,j} \leq X_{2,j} \leq ... \leq X_{M,j} must hold.
Additionally, there are K conditions on the shape of the lines that must be followed. The i-th condition is denoted by (A_i, B_i, C_i), which means:
- If C_i=0, L_{A_i} must visit the immediately lower-left dot for the B_i-th move.
- If C_i=1, L_{A_i} must visit the immediately lower-right dot for the B_i-th move.
That is, X_{A_i, {B_i}+1} = X_{A_i, B_i} + C_i must hold.
In how many ways can Takahashi draw M polygonal lines? Find the count modulo 1000000007.
Notes
Before submission, it is strongly recommended to measure the execution time of your code using "Custom Test".
Constraints
- 1 \leq N \leq 20
- 1 \leq M \leq 20
- 0 \leq K \leq (N-1)M
- 1 \leq A_i \leq M
- 1 \leq B_i \leq N-1
- C_i = 0 or 1
- No pair appears more than once as (A_i, B_i).
Input
Input is given from Standard Input in the following format:
N M K A_1 B_1 C_1 A_2 B_2 C_2 : A_K B_K C_K
Output
Print the number of ways for Takahashi to draw M polygonal lines, modulo 1000000007.
Sample Input 1
3 2 1 1 2 0
Sample Output 1
6
There are six ways to draw lines, as shown below. Here, red lines represent L_1, and green lines represent L_2.

Sample Input 2
3 2 2 1 1 1 2 1 0
Sample Output 2
0
Sample Input 3
5 4 2 1 3 1 4 2 0
Sample Output 3
172
Sample Input 4
20 20 0
Sample Output 4
881396682