Official

B - Insert 1, 2, 3, ... Editorial by evima

Hints → https://atcoder.jp/contests/agc063/editorial/6881

[1] Determining generatability

A sequence is generatable if and only if you can repeatedly remove \((1,2,\ldots,k-1,k)\) from \(a\) to make it empty, looking at the operations in reverse order. Thus, one possible way to determine generatability is to keep deleting \((1,2,\ldots,k-1,k)\) as many times as possible to see if we get an empty sequence.

Here, it is troublesome that there are multiple choices of positions from which \((1,2,\ldots,k-1,k)\) should be deleted, but this position can be uniquely determined as follows.

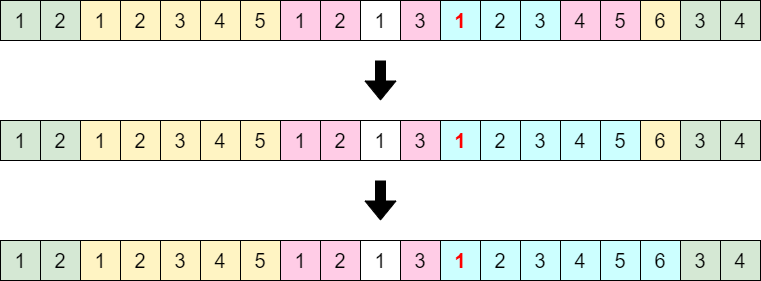
[Proposition] Let \(a\) be a non-empty sequence, and look at the rightmost \(1\) in it. Let \((1, 2, \ldots, k)\) be the maximum-length sequence of consecutive numbers starting from that \(1\), and let \(a'\) be the sequence obtained by deleting that sequence from \(a\). Then, \(a\) is generatable if and only if \(a'\) is generatable.

It is clear that \(a\) is generatable if \(a'\) is generatable.

Suppose \(a\) is generatable, and let \((1,2,\ldots,k)\) be the maximum-length sequence of consecutive numbers starting at the rightmost \(1\). No deletion will be performed to the right of this position until this \(1\) is deleted (since we are looking at the rightmost \(1\)). Thus, if \((1,2,\ldots,k')\) is the sequence that is deleted when this \(1\) is deleted, then \(k'\leq k\) holds.

If \(k'<k\), then some deletion after deleting \((1,2\ldots,k')\) will also delete part of \((k'+1,k'+2,\ldots)\). If we instead delete that part at the same time as deleting the \((1,2,\ldots,k')\) part, we can delete more numbers when deleting the rightmost \(1\). We can repeat this process to obtain a procedure that deletes the maximum-length sequence of consecutive numbers \((1,2,\ldots,k)\) simultaneously.

See also the following figure.

Thus, to determine whether a sequence is generatable, we can repeatedly delete the maximum-length sequence of consecutive numbers starting at the rightmost \(1\). More specifically, using a stack, we can do the following.

[Decision algorithm]

  • Add the elements of the sequence \(a\) to the stack, in order from right to left.
  • When \(1\) is added, remove the maximum-length part with consecutive numbers from the top of the stack.
  • If the stack is empty when all elements of the sequence have been processed, \(a\) is generatable. If it is not empty, then \(a\) is not generatable.

[2] Count up

Counting the number of pairs \((L,R)\) can be done in one of the following two natural ways. Both methods take \(O(N)\) time.

[2-1] Counting with \(L\) fixed

Consider finding the number of \((L,R)\) that satisfy the condition when \(L\) is fixed. The following monotonicity is useful here.

  • If \(L\leq R_1\leq R_2\) and \((L,R_2)\) satisfy the condition, then so does \((L,R_1)\).

From this monotonicity, it is sufficient to find the largest \(R\) that satisfies the condition for each \(L\). This \(R\) can be computed by reading the top of the stack immediately after adding \(A_L\) when [Decision algorithm] in [1] is performed for the whole \(A\) (the top of the stack is the leftmost element that cannot be deleted with elements up to \(A_L\)).

[2-2] Counting with \(R\) fixed

Consider finding the number of \((L,R)\) that satisfy the condition when \(R\) is fixed. The question is how many times the stack will be empty if we apply [Decision algorithm] in [1] to the \((A_1, \ldots, A_R)\) part, starting from \(A_R\).

Let \(\mathrm{dp}[R]\) be the sought number of times. If we assume that the stack becomes empty for the first time immediately after inserting \(A_L\) when [Decision algorithm] is applied to the \((A_1, \ldots, A_R)\) part, we can calculate \(\mathrm{dp}[R] = \mathrm{dp}[L-1] + 1\).

Therefore, all we need to know is when the stack becomes empty for the first time when we apply [Decision algorithm] to the \((A_1, \ldots, A_R)\) part. This is exactly when \(A_R\) is taken out for the first time when [Decision algorithm] is applied to the whole \(A\).

posted:
last update: