Hints → https://atcoder.jp/contests/agc063/editorial/6881

---

[0] Terms and symbols

Treat a pair of non-negative integers as a lattice point on the coordinate plane.

Since it is relatively easy to solve the case in which one of \(a_1,a_2,b_1,b_2\) is \(0\), we assume that \(a_1,a_2,b_1,b_2\) are all positive in the following explanation. Therefore, when we simply say “lattice point”, it is assumed that the \(x\)- and \(y\)-coordinates are positive.

For a lattice point \(A\), the slope of the line \(OA\) is simply called the “slope of \(A\)”.

For positive rational numbers \(l,r\) (\(l<r\)), let \(S(l,r)\) denote the set of all lattice points whose slope is greater than \(l\) and less than \(r\). That is,

\[S(l,r) = \{(x,y)\mid x,y\in \mathbb{Z}_{>0}, l < \frac{y}{x} < r\}.\]

---

[1] With one operation

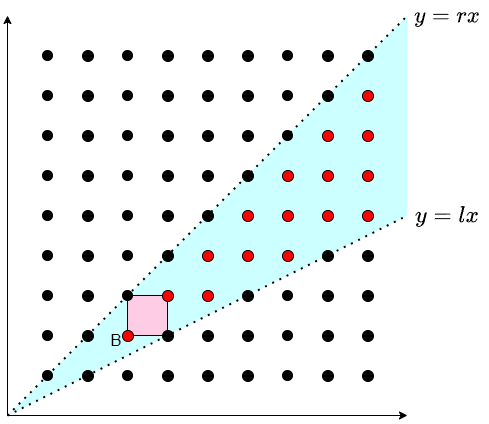
Let \(B(b_1,b_2)\) be a lattice point. Graphically, the operation in question can be expressed as follows: if the half-line \(OA\) intersects the square region \([b_1,b_1+1)\times [b_2,b_2+1)\), then we can move \(A\) to \(B\).

Conversely, if we fix \(B\), we see that the set of all \(A\) that can be moved to \(B\) is a set in the form of \(S(l,r)\). Specifically, we have the following.

[Proposition 1] Let \(B(b_1,b_2)\) be a lattice point, and let \(l = \dfrac{b_2}{b_1+1}\), \(r = \dfrac{b_2+1}{b_1}\). Then, it is possible to get \(B\) from \(A\) with one operation if and only if \(A\in S(l,r)\).

---

[2] With \(k\) operations

Fix a lattice point \(B(b_1,b_2)\) and define the rational numbers \(l_1\) and \(r_1\) as the \(l\) and \(r\) in [Proposition 1], respectively. That is, let \(l_1 = \dfrac{b_2}{b_1+1}\) and \(r_1 = \dfrac{b_2+1}{b_1}\).

Define \(l_k, r_k\) inductively for \(k\geq 2\) as follows:

\[l_{k+1} = \min \biggl\{\frac{y}{x+1}\biggm| (x,y) \in S(l_k,r_k)\biggr\},\qquad r_{k+1} = \max \biggl\{\frac{y+1}{x}\biggm| (x,y) \in S(l_k,r _k)\biggr\}. \]

It is not clear that \(\min\) and \(\max\) exist here, but their existence, along with how to calculate them, will be confirmed in [3]. For now, we accept their existence and continue the argument.

By considering the points neighboring to a lattice point on the line \(y=l_kx\), we can find \(l_{k+1}\leq l_k\). Similarly, \(r_{k+1}\geq r_k\).

[Proposition 2] It is possible to get \(B\) from \(A\) with \(k\) operations if and only if \(A\in S(l_k,r_k)\).

We show this by induction on \(k\). It suffices to show that:

it is possible to move \(A\) to a point in \(S(l_k,r_k)\) with one operation if and only if \(A\in S(l_{k+1},r_{k+1})\).

First, it is easy to see from [Proposition 1] that if \(A\) can be moved to a point in \(S(l_k,r_k)\), then \(A\in S(l_{k+1},r_{k+1})\). Now, assume that \(A \in S(l_{k+1},r_{k+1})\) and show that \(A\) can be moved to a point in \(S(l_k,r_k)\) with one operation. Since it is clear when \(A\in S(l_k,r_k)\), we only need to show it when the slope of \(A\) is in either \((l_{k+1},l_k]\) or \([r_k,r_{k+1})\). These two are similar, so let us assume that it is in \((l_{k+1},l_k]\).

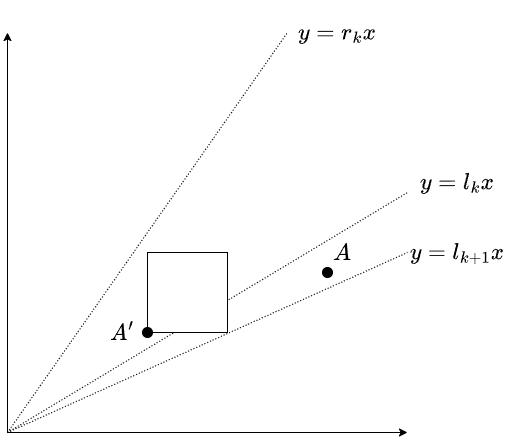
From the definition of \(l_{k+1}\), there is \(A'(x,y) \in S(l_k,r_k)\) such that \(l_{k+1} = \dfrac{y}{x+1}\). From [Proposition 1], the points in \(S\biggl(l_{k+1},\dfrac{y+1}{x}\biggr)\) are the points that can be moved to \(A'\). Since \(A\dfrac{y+1}{x} > \dfrac{y}{x} > l_k\), we have \(A\in S\biggl(l_{k+1},\dfrac{y+1}{x}\biggr)\), so \(A\) can be move to \(A'\). This shows [Proposition 2].

[3] Calculating \(l_{k+1}\) and \(r_{k+1}\)

In the following, when we simply write “rational numbers \(\dfrac{y}{x}\)” and such, we assume that \(x,y\) are positive integers. (We do not assume \(\gcd(x,y)=1\) unless specifically stated.)

Since \(L_{k+1}\) and \(R_{k+1}\) are calculated in the same way, \(R_{k+1}\) is explained here.

[Problem] Let \(l, r\) be positive rational numbers satisfying \(l<r\). Find the maximum value of \(\dfrac{y+1}{x}\) for a rational number \(\dfrac{y}{x}\) satisfying \(l<\dfrac{y}{x}<r\).

The solution to this problem is as follows:

Among the rational numbers \(\dfrac{y}{x}\) such that \(l < \dfrac{y}{x}<r\), take the one with the smallest \(x\). There may be multiple choices for \(y\) if \(x=1\), in which case we take \(y\) to be the largest. Then, \(\dfrac{y+1}{x}\) gives the solution to [Problem].

Let us show this. Take \(\dfrac{y}{x}\) as above. It suffices to show that \(\dfrac{Y+1}{X} \leq \dfrac{y+1}{x}\) for any rational number \(\dfrac{Y}{X}\) satisfying \(l < \dfrac{Y}{X} < r\).

We show this by induction on the denominator \(X\). It is clear when \(X=x\). Suppose that \(\dfrac{Y}{X}\) satisfies \(X\geq x+1\) and \(l < \dfrac{Y}{X} < r\), and assume the assertion for the rational numbers with smaller denominators.

If \(\dfrac{Y}{X}\leq \dfrac{y}{x}\), then \(X(y+1)-x(Y+1)=(Xy-xY)+(X-x) > 0\), so the assertion holds. Now, suppose that \(\dfrac{Y}{X} < \dfrac{Y}{X}\).

It suffices to show the assertion assuming that \(\dfrac{Y}{X}\) is an irreducible fraction. Suppose that, in the Farey sequence up to the denominator \(X\), the left neighbor of \(\dfrac{Y}{X}\) is \(\dfrac{q}{p}\). Then, \(\dfrac{Y}{X}\leq \dfrac{q}{p}< \dfrac{Y}{X}\). From the minimality of \(X\) follows that \(x\leq p < X\). Also, \(pY - qX = 1\) by the property of the Farey sequence.

Then, \((q+1)X-p(Y+1)=(qX-pY)+X-p = X-p-1\geq 0\), which shows \(\dfrac{Y+1}{X} \leq \dfrac{q+1}{p}\). From the inductive assumption, \(\dfrac{q+1}{p} \leq \dfrac{y+1}{x}\) also holds, so \(\dfrac{Y+1}{X}\leq\dfrac{y+1}{x}\) is shown.

---

[4] Summary

In the end, we found that \(l_{k+1}, r_{k+1}\) can be calculated as follows.

• Among the rational numbers \(\dfrac{y}{x}\) such that \(l_k < \dfrac{y}{x} < r_k\), take the one with the smallest \(x\). If \(x=1\), take the one with the largest \(y\). We have \(r_{k+1} = \dfrac{y+1}{x}\).

• Among the rational numbers \(\dfrac{y}{x}\) such that \(l_k < \dfrac{y}{x} < r_k\), take the one with the smallest \(y\). If \(y=1\), take the one with the largest \(x\). We have \(l_{k+1} = \dfrac{y}{x+1}\).

These \(\dfrac{y}{x}\) can be computed by considering the behavior of the Farey sequence (or Stern-Brocot tree).

When \(x=1\) or \(y=1\) is reached, we have \(l_k=l_{k+1}\) and \(r_k=r_{k+1}\), so \(l_k\) and \(r_k\) are constant from there. Therefore, the answer to this problem can be obtained by repeating the above calculation until \(l_k\) and \(r_k\) become constant or \(A\in S(l_k,r_k)\).

---

Finally, we show that \(l_k\) and \(r_k\) converge in \(O(\log (b_1+b_2))\) iterations.

Until \(x=1\) or \(y=1\) is reached, the same rational number \(\dfrac{y}{x}\) is used to compute \(l_{k+1}\) and \(r_{k+1}\). Let \(\dfrac{y_k}{x_k}\) be this rational number, then \(\dfrac{y_{k+1}}{x_{k+1}}\) is the rational number \(\dfrac{y}{x}\) such that \(l_k=\dfrac{y_k}{x_k+1} < \dfrac{y}{x} < \dfrac{y_k+1}{x_k}=r_k\) with the smallest denominator. We show that \(x_{k+1} \leq \dfrac{2x_k+1}{3}\) holds when \(x_k,y_k,x_{k+1},y_{k+1}>1\).

Let \(\dfrac{q}{p}\) and \(\dfrac{s}{r}\) be the left and right neighbors of \(\dfrac{y_{k+1}}{x_{k+1}}\) in the Farey sequence with the denominator at most \(x_{k+1}\). Then, \(x_k+1\geq p + x_{k+1}\) and \(x_k\geq r + x_{k+1}\) hold, and adding them yields \(2x_k + 1\geq p+r+2x_{k+1}\). Since \(p+r=x_{k+1}\), it follows that \(3x_{k+1}\leq 2x_k+1\).

For this and other reasons, \(l_k\) and \(r_k\) converge in \(O(\log (b_1+b_2))\) iterations. Therefore, this problem can be solved in \(O(\log^2(b_1+b_2))\) time per test case. It can also be solved in \(O(\log(b_1+b_2))\) time by exploiting the fact that \(\dfrac{y_{k+1}}{x_{k+1}}\) is usually an ancestor of \(\dfrac{y_k}{x_k}\) in the Stern-Brocot tree.