 /
/ 
Time Limit: 4 sec / Memory Limit: 256 MB
配点 : 800 点
問題文
競プロ幼稚園には1~Nの番号がついたN人の子供がいます。えび先生は、区別できないC個のキャンディーを子供たちに分配することにしました。子供iのはしゃぎ度がx_iの時、キャンディーをa個もらうと子供iのうれしさはx_i^aになります。幼稚園の活発度はN人の子供たちのうれしさの積になります。各子供にキャンディーを非負整数個配ってC個配りきる方法それぞれに対して幼稚園の活発度を計算して、その総和を子供たちのはしゃぎ度x_1,..,x_Nの関数とみてf(x_1,..,x_N)とおきます。A_i,B_i (1≦i≦N)が与えられるので、 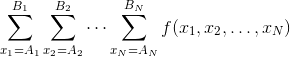 を10^9+7で割ったあまりを求めてください。
を10^9+7で割ったあまりを求めてください。
制約
- 1≦N≦400
- 1≦C≦400
- 1≦A_i≦B_i≦400 (1≦i≦N)
部分点
- A_i=B_i (1≦i≦N) を満たすデータセットに正解した場合は、部分点として400 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N C A_1 A_2 ... A_N B_1 B_2 ... B_N
出力
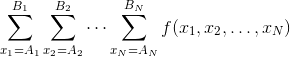 の値を10^9+7で割ったあまりを出力せよ。
の値を10^9+7で割ったあまりを出力せよ。
入力例 1
2 3 1 1 1 1
出力例 1
4
A_i=B_iなので部分点の条件を満たします。 子供1,2のはしゃぎ度が共に1のもの(f(1,1))を考えればよく、この時、
- 子供1に0個,子供2に3個のキャンディーをあげると、幼稚園の活発度は1^0*1^3=1
- 子供1に1個,子供2に2個のキャンディーをあげると、幼稚園の活発度は1^1*1^2=1
- 子供1に2個,子供2に1個のキャンディーをあげると、幼稚園の活発度は1^2*1^1=1
- 子供1に3個,子供2に0個のキャンディーをあげると、幼稚園の活発度は1^3*1^0=1
従ってf(1,1)=1+1+1+1=4となり、fを足し合わせた答えは4です。
入力例 2
1 2 1 3
出力例 2
14
子供が一人なので、子供1のうれしさが幼稚園の活発度になります。また、キャンディの配り方は2つとも子供1にあげる1通りしかないため、この時の幼稚園の活発度はfの値に等しくなります。
- 子供1のはしゃぎ度が1の時、f(1)=1^2=1
- 子供1のはしゃぎ度が2の時、f(2)=2^2=4
- 子供1のはしゃぎ度が3の時、f(3)=3^2=9
従って答えは1+4+9=14となります。
入力例 3
2 3 1 1 2 2
出力例 3
66
f(1,1)=4 , f(1,2)=15 , f(2,1)=15 , f(2,2)=32 となることがわかるので、答えは4+15+15+32=66になります。
入力例 4
4 8 3 1 4 1 3 1 4 1
出力例 4
421749
部分点の条件を満たします。
入力例 5
3 100 7 6 5 9 9 9
出力例 5
139123417
Score : 800 points
Problem Statement
12:17 (UTC): The sample input 1 and 2 were swapped. The error is now fixed. We are very sorry for your inconvenience.
There are N children in AtCoder Kindergarten, conveniently numbered 1 through N. Mr. Evi will distribute C indistinguishable candies to the children.
If child i is given a candies, the child's happiness will become x_i^a, where x_i is the child's excitement level. The activity level of the kindergarten is the product of the happiness of all the N children.
For each possible way to distribute C candies to the children by giving zero or more candies to each child, calculate the activity level of the kindergarten. Then, calculate the sum over all possible way to distribute C candies. This sum can be seen as a function of the children's excitement levels x_1,..,x_N, thus we call it f(x_1,..,x_N).
You are given integers A_i,B_i (1≦i≦N). Find 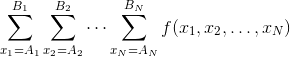 modulo 10^9+7.
modulo 10^9+7.
Constraints
- 1≦N≦400
- 1≦C≦400
- 1≦A_i≦B_i≦400 (1≦i≦N)
Partial Score
- 400 points will be awarded for passing the test set satisfying A_i=B_i (1≦i≦N).
Input
The input is given from Standard Input in the following format:
N C A_1 A_2 ... A_N B_1 B_2 ... B_N
Output
Print the value of 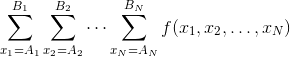 modulo 10^9+7.
modulo 10^9+7.
Sample Input 1
2 3 1 1 1 1
Sample Output 1
4
This case is included in the test set for the partial score, since A_i=B_i. We only have to consider the sum of the activity level of the kindergarten where the excitement level of both child 1 and child 2 are 1 (f(1,1)).
- If child 1 is given 0 candy, and child 2 is given 3 candies, the activity level of the kindergarten is 1^0*1^3=1.
- If child 1 is given 1 candy, and child 2 is given 2 candies, the activity level of the kindergarten is 1^1*1^2=1.
- If child 1 is given 2 candies, and child 2 is given 1 candy, the activity level of the kindergarten is 1^2*1^1=1.
- If child 1 is given 3 candies, and child 2 is given 0 candy, the activity level of the kindergarten is 1^3*1^0=1.
Thus, f(1,1)=1+1+1+1=4, and the sum over all f is also 4.
Sample Input 2
1 2 1 3
Sample Output 2
14
Since there is only one child, child 1's happiness itself will be the activity level of the kindergarten. Since the only possible way to distribute 2 candies is to give both candies to child 1, the activity level in this case will become the value of f.
- When the excitement level of child 1 is 1, f(1)=1^2=1.
- When the excitement level of child 1 is 2, f(2)=2^2=4.
- When the excitement level of child 1 is 3, f(3)=3^2=9.
Thus, the answer is 1+4+9=14.
Sample Input 3
2 3 1 1 2 2
Sample Output 3
66
Since it can be seen that f(1,1)=4 , f(1,2)=15 , f(2,1)=15 , f(2,2)=32, the answer is 4+15+15+32=66.
Sample Input 4
4 8 3 1 4 1 3 1 4 1
Sample Output 4
421749
This case is included in the test set for the partial score.
Sample Input 5
3 100 7 6 5 9 9 9
Sample Output 5
139123417