 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 900 点
問題文
Aliceは数直線の上に住んでいます。今日はある不思議な乗り物に乗って目的地まで行くことを考えました。 はじめ、Aliceは目的地から D 離れたところにいます。Aliceが乗り物にある数 x を入力すると、現在地から目的地に向かって x 進んだところが現在地より目的地に近いとき移動し、そうでないときは動きません。現在地から目的地までの距離が x 未満のとき、x 進んだところは目的地を通りすぎていることに注意してください。また、目的地を通り過ぎると進行方向が変わること、進行方向は何度も変わることがあることに注意してください。
Aliceは乗り物に N 回だけ数を入力し、i 番目に入力する数は d_i の予定でした。Aliceは入力する予定数の書かれたリストを作っておき、その数を 1 つずつ入力します。
しかしイタズラ好きの魔法使いが現れ、Aliceが N 回の入力による移動を終えても目的地にたどり着かないよう、リストの数を 1 つだけ書き換えることを考えました。
魔法使いはイタズラの実行のため以下の Q 個の計画を考えています。
- q_i 回目に入力する数のみをある正整数に変更することで、Aliceが目的地にたどり着かないようにする
Q 個の計画それぞれが実行可能であるか答えるプログラムを書いてください。
制約
- 1≦ N ≦ 5*10^5
- 1≦ Q ≦ 5*10^5
- 1≦ D ≦ 10^9
- 1≦ d_i ≦ 10^9(1≦i≦N)
- 1≦ q_i ≦ N(1≦i≦Q)
- d_i, Dは整数である
入力
入力は以下の形式で標準入力から与えられる。
N D d_1 d_2 ... d_N Q q_1 q_2 ... q_Q
出力
i 番目の計画が実行可能ならYES、そうでないならNOと i 行目に出力せよ。
入力例 1
4 10 3 4 3 3 2 4 3
出力例 1
NO YES
3 番目までの入力でAliceはすでに目的地にたどり着いているため、1 番目の計画の答えはNOです。
例えば、3 番目の入力を 5 にすると、Aliceは以下のような移動をし、目的地にたどり着くことはできないため、2 番目の計画の答えはYESです。
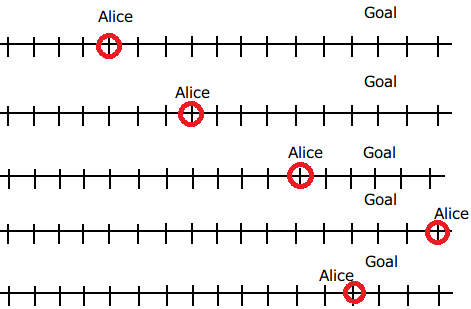
入力例 2
5 9 4 4 2 3 2 5 1 4 2 3 5
出力例 2
YES YES YES YES YES
もともと入力する予定のままでもAliceは目的地にたどり着けないため、すべての計画は実行可能です。
入力例 3
6 15 4 3 5 4 2 1 6 1 2 3 4 5 6
出力例 3
NO NO YES NO NO YES
Score : 900 points
Problem Statement
Alice lives on a line. Today, she will travel to some place in a mysterious vehicle. Initially, the distance between Alice and her destination is D. When she input a number x to the vehicle, it will travel in the direction of the destination by a distance of x if this move would shorten the distance between the vehicle and the destination, and it will stay at its position otherwise. Note that the vehicle may go past the destination when the distance between the vehicle and the destination is less than x.
Alice made a list of N numbers. The i-th number in this list is d_i. She will insert these numbers to the vehicle one by one.
However, a mischievous witch appeared. She is thinking of rewriting one number in the list so that Alice will not reach the destination after N moves.
She has Q plans to do this, as follows:
- Rewrite only the q_i-th number in the list with some integer so that Alice will not reach the destination.
Write a program to determine whether each plan is feasible.
Constraints
- 1≤ N ≤ 5*10^5
- 1≤ Q ≤ 5*10^5
- 1≤ D ≤ 10^9
- 1≤ d_i ≤ 10^9(1≤i≤N)
- 1≤ q_i ≤ N(1≤i≤Q)
- D and each d_i are integers.
Input
Input is given from Standard Input in the following format:
N D d_1 d_2 ... d_N Q q_1 q_2 ... q_Q
Output
Print Q lines. The i-th line should contain YES if the i-th plan is feasible, and NO otherwise.
Sample Input 1
4 10 3 4 3 3 2 4 3
Sample Output 1
NO YES
For the first plan, Alice will already arrive at the destination by the first three moves, and therefore the answer is NO.
For the second plan, rewriting the third number in the list with 5 will prevent Alice from reaching the destination as shown in the following figure, and thus the answer is YES.

Sample Input 2
5 9 4 4 2 3 2 5 1 4 2 3 5
Sample Output 2
YES YES YES YES YES
Alice will not reach the destination as it is, and therefore all the plans are feasible.
Sample Input 3
6 15 4 3 5 4 2 1 6 1 2 3 4 5 6
Sample Output 3
NO NO YES NO NO YES