Official

D - Inc, Dec - Decomposition Editorial by evima

We will explain two approaches.

  1. \(\Theta(N\log N)\) solution by accelerating DP: this article
  2. \(\Theta(N)\) solution by examining the structure of the optimal solution: https://atcoder.jp/contests/arc123/editorial/2321

◆ Reorganizing the problem

The problem asks us to choose the best set of \(2n\) integers \(B_i\) and \(C_i\), but fixing \(B_i\) will automatically fix \(C_i\), so let us rephrase the problem into setting \(n\) integers.

In the end, it turns out that we need to solve a problem in the following form:

  • Given are constant numbers \(a_i\) and \(b_i\).
  • Find the minimum possible value of \(\sum |x_i| + |x_i - b_i|\) when setting integers \(x_1, x_2, \ldots, x_N\) so that \(x_i + a_i \leq x_{i+1}\) holds.

Below, we use these symbols \(x_i, a_i, b_i\).

◆ Calculating the answer with DP

Let \(\text{dp}_n(x)\) be the minimum possible value of \(\sum_{1\leqq i\leqq n}\bigl(|x_i| + |x_i-b_i|\bigr)\) when setting \(x_1, \ldots, x_n\) so that \(x_i + a_i \leq x_{i+1}\) and \(x_n = x\).

The following recurrence formula culculates \(\text{dp}_n(x)\):

  • \(\text{dp}_1(x) = |x| + |x - b_i|\)
  • \(\text{dp}_{n+1}(x) = \min_{y\leqq x - a_i}\text{dp}_n(y) + |x| + |x-b_i|\)

However, \(x\) can take infinitely many values in the first place, so we cannot directly maintain the value \(\text{dp}_n(x)\) for every \(x\). Let us consider some other way to maintain information equivalent to \(\text{dp}_n(x)\).

◆ Functional representation based on changes in slope

We can see that the functions \(\text{dp}_n\) that appear in the above process are convex functions that are concatenations of linear functions with integer slope.

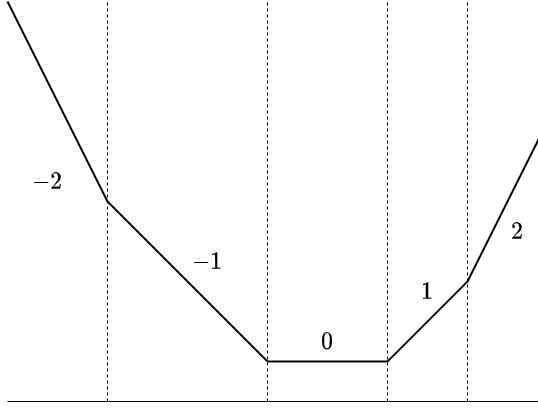
We can represent these functions using the set of coordinates where the slope changes, which enables us to efficiently process the operations on functions described below.

This method of handling convex functions that are concatenations of linear functions is called the slope trick. Below are some references:

◆ Operations needed in this problem

Let us sort out the operations needed to obtain \(\text{dp}_{n+1}\) from \(\text{dp}_n\).

Let \(f = \text{dp}_n\) and \(g = \text{dp}_{n+1}\). Remember that their relation can be represented as \(g(x) = \min_{y\leqq x - a_i}f(y) + |x| + |x-b_i|\). We can decompose the process of obtaining \(g\) from \(f\) as follows:

  • \(f_1(x) = f(x + a_i)\)
  • \(f_2(x) = \min_{y\leqq x - a_i}f(y) = \min_{y\leqq x}f(y - a_i) = \min_{y\leqq x}f_1(y)\)
  • \(g(x) = f_2(x) + |x| + |x - b_i|\)

That is, we can obtain \(g\) from \(f\) by performing the following:

  • translation;
  • “accumulated” \(\min\);
  • addition of the form \(|x-a|\).

These are basic operations in the slope trick, which can be done efficiently with priority queues.

The whole problem can be solved in \(\Theta(N\log N)\) time.

◆ Sample Implementation

posted:
last update: