B - AtCoder Language 解説 by evima
Note: We have a “How to come up with the solution” section at the end of the explanation. Please read it after going through the main text.
Step 1
First, the following two statements are exactly the same:
- All \(K\)-character subsequences are different.
- There are at least \(N-K\) characters between any two identical characters.
Therefore, the number of strings satisfying condition 2, modulo \(998244353\), is the answer.
Example 1
Consider the \(5\)-character string abacb for \(K = 4\).
- All \(4\)-character subsequences of
abacbare different, so 1. is Yes. - As for two identical characters, we have “1st and 3rd characters” and “2nd and 5th characters”, but in both cases, there are at least \(5-4=1\) characters in between, so 2. is also Yes.
Example 2
Consider the \(5\)-character string abacb for \(K = 3\).
- For the \(3\)-character subsequences of
abacb, extracting the 1st, 4th, and 5th characters givesacb, and extracting the 3rd, 4th, and 5th characters also givesacb, making them the same, so 1. is No. - As for two identical characters, we have “1st and 3rd characters” and “2nd and 5th characters”, but the former does not have at least \(5-3=2\) characters in between, so 2. is also No.
Proof (If 2. is No, then 1. is also No)
If 2. is No, you can obtain two identical \(K\)-character subsequences in the following way, making 1. also No.
- Assume the \(a\)-th and \(b\)-th characters of the string are the same, and there are less than \(N-K\) characters in between.
- Consider the following two subsequences:
- (a) A subsequence obtained by extracting the \(1, 2, \dots, a-1,a, b+1, \dots, N\)-th characters of the string.
- (b) A subsequence obtained by extracting the \(1, 2, \dots, a-1,b, b+1, \dots, N\)-th characters of the string.
- (a) and (b) are the same as strings and have at least \(K\) characters, so the first \(K\) characters of (a) and (b) are two identical \(K\)-character subsequences.
For example, in the case of the string codeforces, you can obtain two identical \(5\)-character subsequences as shown below. Note that \(N = 10, K = 5\) in this case.
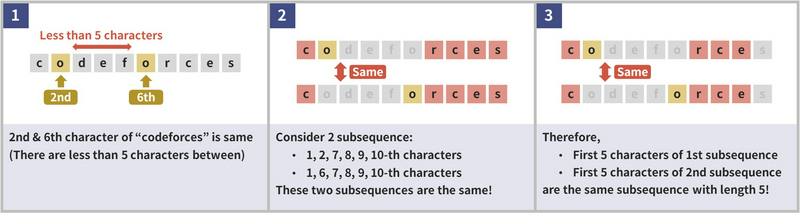
Proof (If 1. is No, then 2. is also No)
If 1. is No, specifically, consider the following two subsequences (extracted from different positions) are the same:
- A subsequence obtained by extracting the \(s_1, s_2, \dots, s_K\)-th characters of the string in order.
- A subsequence obtained by extracting the \(t_1, t_2, \dots, t_K\)-th characters of the string in order.
In this case, \(|t_i - s_i| \leq N - K\) holds for all \(i\). The reason is as follows. Note that we assume \(s_i \leq t_i\) for the proof, but if not, you can prove it by reversing \(s\) and \(t\).
- Since \(s_i\) is the \(i\)th character from the beginning of the subsequence, \(s_i \geq i\).
- Since \(t_i\) is the \((K-i+1)\)th character from the end of the subsequence, \(t_i \leq N-K+i\).
- Therefore, \(t_i - s_i \leq N-K\).
Since the subsequences \(s\) and \(t\) are extracted from different positions, there is an \(i\) such that \(s_i \neq t_i\). However, even for such \(i\), we have \(|t_i - s_i| \leq N - K\), indicating that there are less than \(N-K\) characters between two identical characters, and thus 2. is No.
Step 2
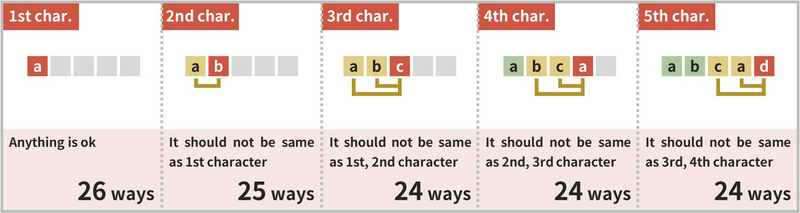
So, how many strings of AtCoder language characters are there such that there are at least \(N-K\) characters between any two identical characters? Let’s first consider an example where \(N = 5, K = 3\), and there are \(26\) characters from a to z. Considering the characters in the order of the 1st, 2nd, 3rd, 4th, and 5th positions,
- The 1st character can be anything, so \(26\) ways.
- The 2nd character must not be the same as the 1st, so \(25\) ways.
- The 3rd character must not be the same as the 1st or 2nd, so \(24\) ways.
- The 4th character must not be the same as the 2nd or 3rd, so \(24\) ways.
- The 5th character must not be the same as the 3rd or 4th, so \(24\) ways.
This results in \(26 \times 25 \times 24 \times 24 \times 24 = 8985600\) ways.
Similarly, for the general case, the number of ways to decide the \(i\)-th character is as follows:
- If \(i \leq N-K\): \(\max(0, L+1-i)\) ways.
- If \(i > N-K\): \(\max(0, L-(N-K))\) ways.
Therefore, writing a program as shown in the following sample implementation will get you AC. The time complexity is \(O(N)\), which fits within the execution time limit since the problem constraints have \(N \leq 500000\).
Sample Implementation (C++)
#include <iostream>
using namespace std;
const long long mod = 998244353;
long long N;
long long K;
long long L;
long long Answer;
int main() {
// Step 1. Input
cin >> N >> K >> L;
// Step 2. Calculation
Answer = 1;
for (int i = 1; i <= N; i++) {
if (i <= N - K) {
Answer *= max(0LL, L + 1 - i);
}
else {
Answer *= max(0LL, L - (N - K));
}
Answer %= mod; // Take mod every time to prevent overflow
}
// Step 3. Output
cout << Answer << endl;
return 0;
}
Sample Implementation (Python)
# Step 1. Input
N, K, L = map(int, input().split())
# Step 2. Calculation
Answer = 1
for i in range(1, N + 1):
if i <= N - K:
Answer *= max(0, L + 1 - i)
else:
Answer *= max(0, L - (N - K))
Answer %= 998244353 # Take mod every time to prevent overflow
# Step 3. Output
print(Answer)
Supplement: How to come up with the solution?
Some of you might think that coming up with the solution to this problem requires genius inspiration. Particularly, the observation in Step 1 might feel quite non-trivial and hard to come up with. However, following the appropriate steps makes it possible to come up with the solution even without any sudden inspiration.
View explanation
First, consider the case of \(K = 1\), specifically \((N, K, L) = (4, 1, 26)\).
- In this case, all characters must be different.
- Therefore, the answer is calculated as \(26 \times 25 \times 24 \times 23\).
Next, consider the case of \(K = 2\), specifically \((N, K, L) = (4, 2, 26)\).
- Of course, if all characters are different, it clearly satisfies the condition.
- But what about other cases?
- For instance, in the string
java, the subsequences of the 1st, 2nd characters and the 1st, 4th characters are the same, not satisfying the condition. - Similarly, in the string
kiss, the subsequences of the 1st, 3rd characters and the 1st, 4th characters are the same, not satisfying the condition.
- For instance, in the string
- Thinking this way, it becomes clear that most cases do not satisfy the condition.
- However, upon further consideration, it is found that cases where only the first and last characters are the same, such as
aqua, are exceptions. - Therefore, the answer is calculated as \(26 \times 25 \times 24 \times 24\).
Let’s think about why only the cases where the first and last characters are the same are exceptions.
- Assume the \(a\)-th and \(b\)-th characters are the same \((a < b)\).
- If \(a \neq 1\), the subsequences of the 1st, \(a\)-th characters and the 1st, \(b\)-th characters are the same, not satisfying the condition.
- If \(b \neq N\), the subsequences of the \(a\)-th, \(N\)-th characters and the \(b\)-th, \(N\)-th characters are the same, not satisfying the condition.
- However, if \((a, b) = (1, N)\), such subsequences cannot be formed, making it an exception.
Can we apply this reasoning to the case of \(K=3\)?
- Assume the \(a\)-th and \(b\)-th characters are the same \((a < b)\).
- If \(a \geq 3\), the subsequences of the 1st, 2nd, \(a\)-th characters and the 1st, 2nd, \(b\)-th characters are the same, not satisfying the condition.
- If \(b \leq N - 2\), the subsequences of the \(a\)-th, \((N-1)\)-th, \(N\)-th characters and the \(b\)-th, \((N-1)\)-th, \(N\)-th characters are the same, not satisfying the condition.
- If \(a \geq 2\) and \(b \leq N - 1\), the subsequences of the 1st, \(a\)-th, \(N\)-th characters and the 1st, \(b\)-th, \(N\)-th characters are the same, not satisfying the condition.
- Other strings such as
pastaorstarsseem to satisfy the condition. - Let’s summarize the aforementioned three conditions.
- In summary, it is found that the condition is not satisfied when \(b-a \leq N-3\).
- In other words, the condition is not satisfied when the interval between two identical characters is less than \(N-3\) characters.
This brings us very close to Step 1. With this line of reasoning, solving for \(K \geq 4\) should not be too difficult.
In competitive programming, considering how the answer changes with small inputs can naturally lead to solving the problem. This technique is frequently used in ARC, so I recommend remembering it.
投稿日時:
最終更新: