G - 魔方陣
Editorial
 /
/ 
 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
問題文
高橋君は魔方陣が大好きです。
魔方陣というのは3マス×3マスの方陣に相異なる正の整数を配置して、タテ・ヨコ・ナナメいずれの列についても、その列の 3 つの整数の和が等しくなっているようなものの事です。
高橋君はふと、 3 つの和が等しいのではなく 3 つの積が等しいような「積バージョンの魔方陣」が作れるのではないかと思いました。
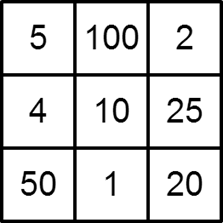
がんばって模索したところ、下図のような積バージョンの魔方陣を1つ作ることが出来ました。

ナナメも含めたすべての列の積が 1000 になっています。
高橋君は今度は中央のマスが N であるような積バージョンの魔方陣は何種類あるのか気になりました。
ここで 90 度回転や左右反転などによって変換できる 2 つの魔方陣は区別しないとします。
高橋君のために、中央のマスが N であるような積バージョンの魔方陣の種類を求めてください。
入力
入力は以下の形式で標準入力から与えられる
N
- 1 行目には積バージョンの魔方陣の中央の値 N (1 ≦ N ≦ 10^{12}) が与えられる。
出力
中央のマスが N であるような積バージョンの魔方陣の種類を 1 行で出力せよ。 出力の末尾には改行をいれること。
入力例1
16
出力例1
1
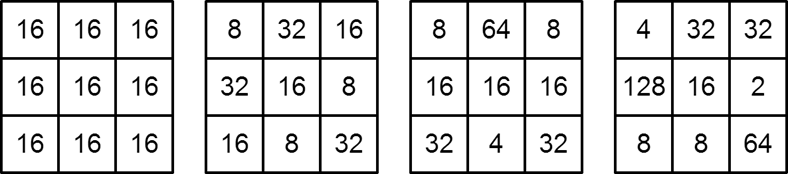
以下の様なパターンは配置されている整数が重複しているので魔方陣ではありません。

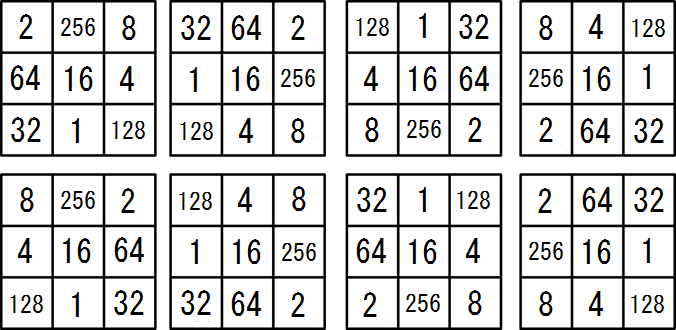
以下の様なパターンは全て回転や反転によって同じものに変換することができます。

入力例2
10
出力例2
1
入力例3
9
出力例3
0
入力例4
90
出力例4
29