 /
/ 
Time Limit: 8 sec / Memory Limit: 256 MB
Problem
Wolf Sothe owns a long land in the jungle. In this linear land, N trees grow at regular intervals. The size of the i_{th} tree from one end is given as t_i.
Inside the jungle it is dark because trees obstruct sunlight. In order to let sunlight shine into the jungle, Wolf Sothe considers cutting some of the N trees (or cutting no one). More specifically, trees will be cut with the following rules.
- Up to M trees can be cut (no more than M).
- Considering the impact on the surrounding ecosystem, it is not allowed to cut two or more trees in arbitrary K consecutive trees. More precisely, there is not i(1≦i≦N-K+1) such that 2 or more trees are cut in the i_{th}, (i + 1)_{th}, ......, (i + K-1)_{th} trees from one end.
- If Wolf Sothe cuts the i_{th} tree from one end, the size of the tree t_i becomes 0.
- We want the maximum value of the sum of sizes of K consecutive trees to be as small as possible. Namely, we want to minimize
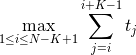 .
.
Since the size of the N trees and M, K have been given, when we make the optimal cutting choice for the trees, please obtain the minimum value of the maximum value of the sum of sizes of consecutive K trees.
Input
Inputs will be given by standard input in following format.
N M K t_1 t_2 : t_N
- At the first line, integer N(1≦N≦100,000), M(1≦M≦N), K(1≦K≦N) will be given.
- From the second line there are N additional lines to give information about sizes of trees. At the i_{th} line, integer t_i(1≦t_i≦1,000,000,000) will be given.
Output
Please print the minimum value of the maximum value of the sum of sizes of consecutive K trees, when we made the optimal cutting choice for the trees in a line.
Print a newline at the end of output.
Input Example 1
6 2 3 1 5 6 2 4 3
Output Example 1
7
If Wolf Sothe cuts the 3_{rd} and 6_{th} tree, the minimum value of the maximum value of the sum of sizes of consecutive 3 consecutive trees will be obtained when it is for the 2_{nd}, 3_{rd}, 4_{th} tree. The sum of sizes is 5+0+2=7.
Input Example 2
10 3 4 3 14 1 5 9 2 6 5 3 5
Output Example 2
17