 /
/ 
Time Limit: 5 sec / Memory Limit: 256 MB
問題文
あなたはDISCO社の面接を受けています。面接前に 0 個のノードからなる二分探索木 T をあなたは与えられました。
あなたは面接官から以下の Q 個のクエリを与えられた順序で処理しなさいというお題を与えられました。あなたは、 Q 個のクエリを高速に処理して面接官を驚かせることにしました。
クエリの種類を以下に示します。
1 v: T に値が v であるようなノードを適切な位置に挿入せよ。2 v: T に含まれる値が v であるようなノード u の左部分木 lst と右部分木 rst について、高さの差 h(lst) - h(rst) を出力せよ。3 v: T に含まれる値が v であるようなノード u に左の子ノードが存在したならば、 u を右回転せよ。左の子ノードが存在しなかったならば-1を出力せよ。4 v: T に含まれる値が v であるようなノード u に右の子ノードが存在したならば、 u を左回転せよ。右の子ノードが存在しなかったならば-1を出力せよ。
上記の種類 1 のクエリにおいて、値が v であるようなノードが T に存在しないことが保証されます。 上記の種類 2,3,4 のクエリにおいて、値が v であるようなノードが T に存在することが保証されます。
-
ここで、二分探索木 T の高さは以下のように定義される。
- あるノード u を根とする二分探索木の高さ h(u) は u の左部分木 lst と u の右部分木 rst としたとき、 h(u) = max(h(lst), h(rst))+1 で表される。
- ここで、 u に左部分木 lst が存在しないときは h(lst) = 0 として扱う。
- 同様に、 u に右部分木 rst が存在しないときは h(rst) = 0 として扱う。
-
二分探索木 T へノード u を挿入する操作は以下のようにして行われる。なお、この操作の結果は T と u が与えられたとき一意に定まることが保証されている。
- T が 0 個のノードからなるとき、 T を u を根とする二分探索木にし処理を終了する。
-
T が 1 個以上のノードからなるとき、以下の条件を満たすように u をあるノードの子にし、処理を終了する。
- あるノード w が持つ直接の子の数は最大でもたかだか 2 つである(これはそれぞれ左の子、右の子と呼ばれる)。
- あるノード w の左の子孫であるようなノードが持つ値はどれも w の値未満である。
- あるノード w の右の子孫であるようなノードが持つ値はどれも w の値以上である。
-
二分探索木 T に含まれるノード u の右回転は以下のようにして行われる。この操作は u に左の子が存在しないとき行うことはできない。
- u の左の子を l とする。
- u と l をつなぐ辺を削除する。また、 u に親 p が存在するとき、 u と p をつなぐ辺を削除し、 p を l の親となるように接続する。
- l に右の子 r が存在するならば、 l と r をつなぐ辺を削除し、 r を u の左の子となるように接続する。
- u を l の右の子となるように接続する。
-
二分探索木 T に含まれるノード u の左回転は以下のようにして行われる。この操作は u に右の子が存在しないとき行うことはできない。
- u の右の子を r とする。
- u と r をつなぐ辺を削除する。また、 u に親 p が存在するとき、 u と p をつなぐ辺を削除し、 p を r の親となるように接続する。
- r に左の子 l が存在するならば、 r と l をつなぐ辺を削除し、 l を u の右の子となるように接続する。
- u を r の左の子となるように接続する。
入力
入力は以下の形式で標準入力から与えられる。
Q t_1 v_1 . . . t_Q v_Q
- 1 行目に 1 行にクエリの数を表す整数 Q (1≦Q≦400,000) が与えられる。
- 続く Q 行のち i 行目では i 番目のクエリの種類と、ノードの値を表す整数 t_i, v_i(1≦t_i≦4,1≦v_i≦400,000) が空白区切りで与えられる。
- 種類 1 のクエリにおいて、値が v であるようなノードが T 中に存在しないことが保証される。
- 種類 2,3,4 のクエリにおいて、値が v であるようなノードが T 中に存在することが保証される。
出力
各クエリの結果を与えられた順に 1 行ごとに出力せよ。出力する場合は以下の 3 種類であることに注意せよ。
- 種類 2 のクエリ
- 種類 3 のクエリにおいて、値が v であるようなノード u に左の子が存在しなかった場合
- 種類 4 のクエリにおいて、値が v であるようなノード u に右の子が存在しなかった場合
部分点
この問題には部分点が設定されている。
- 1≦Q≦1,000 を満たすようなデータセットに正解した場合 20 点が与えられる。
- 1≦t_i≦2(1≦i≦Q) を満たすようなデータセットに正解した場合上記の部分点とは別に 30 点が与えられる。
- 追加制約のないデータセットに正解した場合さらに 100 点が得られ合計 150 点が得られる。
入力例 1
13 1 4 1 2 1 1 1 3 1 6 1 5 1 7 1 8 2 1 2 2 2 4 2 6 2 7
出力例 1
0 0 -1 -1 -1
- 1 番目から 8 番目までのクエリにおいて T にノードをクエリで与えられた順序に従って挿入します。挿入の際、回転操作は行われないことに注意してください。
- 以下の図に 8 番目のクエリが行われた後の T を示します。
- ノード内に書かれた値は、ノードが持つ値を、ノードの横に書かれた値はそのノードを根とする部分木の高さを示します。
- 与えられたクエリによって T の形状は一意に定まることが保証されます。
- 9 番目のクエリにおいて、値が 1 であるようなノードの左部分木の高さ h(lst) と右部分木の高さ h(rst) はともに 0 なので h(lst)-h(rst)は 0 です。
- 10 番目のクエリにおいて、 h(lst) と h(rst) はともに 1 なので h(lst)-h(rst)は 0 です。
- 11 番目のクエリにおいて、 h(lst) は 2 、 h(rst) は 3 なので h(lst)-h(rst)は -1 です。
- 12 番目のクエリにおいて、 h(lst) は 1 、 h(rst) は 2 なので h(lst)-h(rst)は -1 です。
- 13 番目のクエリにおいて、 h(lst) は 0 、 h(rst) は 1 なので h(lst)-h(rst)は -1 です。
- 子が存在しないような部分木の高さは 0 となることに注意してください。
- このケースは 2 つの部分点制約の両方の部分点制約を満たします。
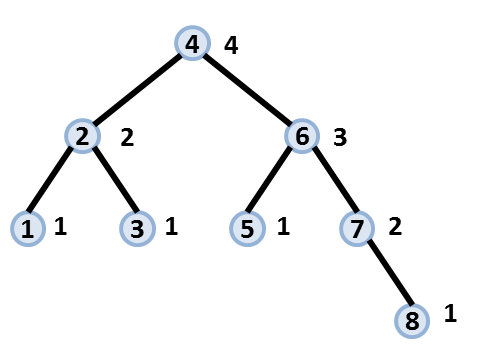
図 1 : 8 番目のクエリ終了時点での T の様子
入力例 2
14 1 4 1 2 1 1 1 3 1 6 1 5 1 7 1 8 3 4 2 2 2 4 2 6 2 7 3 7
出力例 2
-3 -2 -1 -1 -1
- 以下の図に 9 番目のクエリにより右回転が行われる前の T を左に、回転後の T を右に示します。
- ノード同士の位置関係の変化に注意してください。
- 14 番目のクエリにおいて、 値が 7 であるようなノードに左の子は存在しないため、
-1を出力してください。 - 与えられたクエリによって T の形状は一意に定まることが保証されます。
- このケースは 1 つ目の部分点制約を満たします。
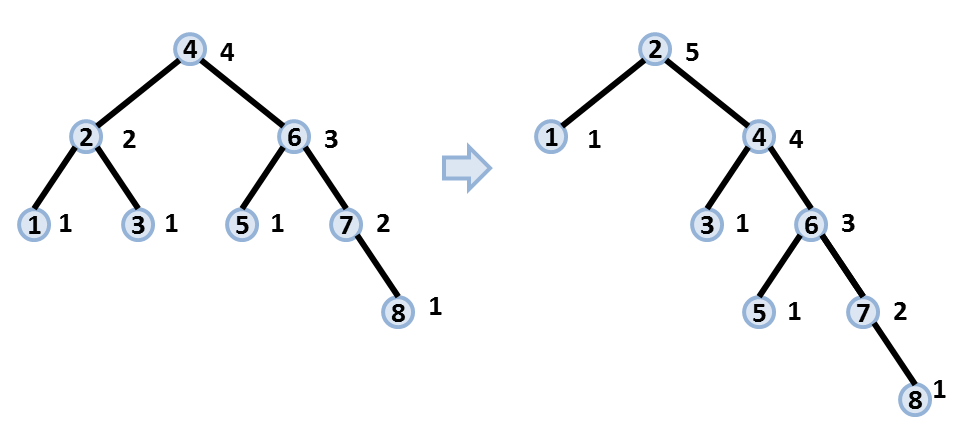
図 2 : 9 番目のクエリによる T の変形の様子
入力例 3
14 1 4 1 2 1 1 1 3 1 6 1 5 1 7 1 8 4 6 2 2 2 4 2 6 2 7 4 6
出力例 3
0 -1 1 1 -1
- 以下の図に 9 番目のクエリにより左回転が行われる前の T を左に、回転後の T を右に示します。
- ノード同士の位置関係の変化に注意してください。
- 14 番目のクエリにおいて、 値が 6 であるようなノードに右の子は存在しないため、
-1を出力してください。 - 与えられたクエリによって T の形状は一意に定まることが保証されます。
- このケースは 1 つ目の部分点制約を満たします。
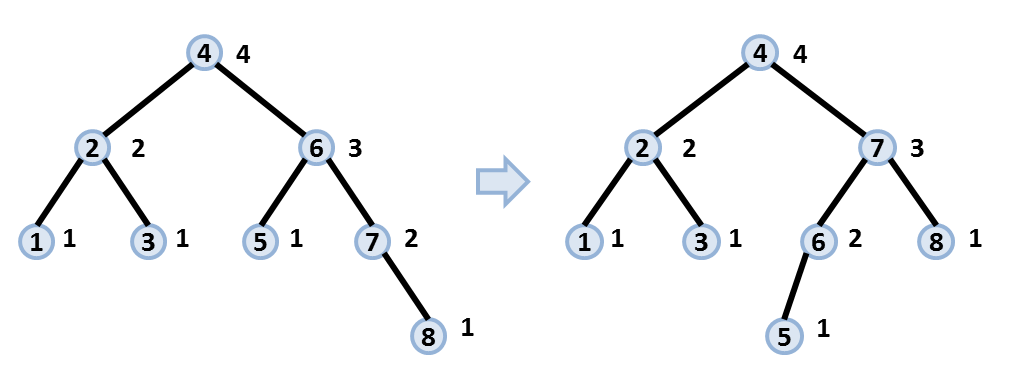
図 3 : 9 番目のクエリによる T の変形の様子