 /
/ 
Time Limit: 1 sec / Memory Limit: 256 MB
配点 : 300 点
問題文
Eli- 1 さんは仕事時間が N 秒のティッシュ配りのバイトをすることにした. Eli- 1 さんは特殊能力である分身を利用してなるべく多くのティッシュを配ることにした. Eli- gen さんができる行動は次の 2 種類である.
- gen \times C ( C は分身にかかる時間の係数) 秒をかけてEli- gen さんとEli- (gen + 1) さんの 2 人に分身する.
- 世代( = gen )に関わらず 1 秒をかけてちょうど 1 個のティッシュを配る.
配りながら分身するということはできない. N , C が与えられたとき, Eli- 1 さんが分身と合計で最大何個のティッシュを配ることができるかを求めよ. ただし, 配れるティッシュの数は非常に大きくなることがあるため 1000000007 (= 10^9 + 7) で割った余りを解答として出力せよ.
制約
- 1 \leq Q \leq 100000 = 10^5
- 1 \leq N_q \leq 100000 = 10^5
- 1 \leq C_q \leq 20000 = 2 \times 10^4
入力
入力は以下の形式で標準入力から与えられる.
Q N_1 C_1 : N_Q C_Q
入力は複数のクエリからなる. 1 行目には, クエリの個数を表す整数 Q が与えられる.
続く Q 行に, それぞれ 1 個のクエリが与えられる. q ( 1 \leq q \leq Q ) 番目のクエリでは, N_q と C_q が半角スペース区切りで与えられる. N_q と C_q は q 番目のクエリにおける, 仕事時間と分身にかかる時間の係数をそれぞれ表している.
出力
各クエリに対して, Eli- 1 さんが分身と合計で最大何個のティッシュを配ることができるかを 1 行で出力せよ. ただし, 配れるティッシュの数は非常に大きくなることがあるため 1000000007 ( = 10^9 + 7 ) で割った余りを出力せよ.
部分点
Q = 1 を満たすデータセットに正解した場合は 30 点の部分点が与えられる.
追加制約のないデータセットに正解した場合は追加で 270 点が与えられ,合計で 300 点が得られる.
入力例 1
2 20 8 20 12
出力例 1
24 20
1 つめのクエリでは, 分身しないと 20 個しか配れないところを, 分身後 2 人が 12 個ずつ配ることで 24 個配ることができ, これが最大である.
2 つめのクエリでは, 分身しても 2 人がそれぞれ 8 個ずつしか配れないため, 分身せずに 20 個配るほうがよい.
入力例 2
1 20 3
出力例 2
67
以下の図のようにすればよい. 黒線は分身を表し, 赤線はティッシュを配ることを表している.
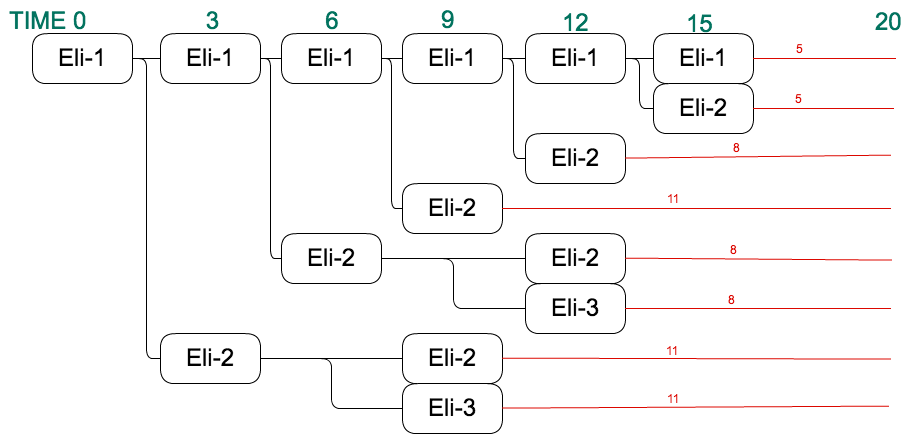
このケースは部分点の追加制約を満たす.
入力例 3
1 200 1
出力例 3
148322100
1000000007 ( 10^9 + 7 ) で割った余りを出力する必要があることに注意せよ.
このケースは部分点の追加制約を満たす.
Score : 300 points
Problem Statement
Eli- 1 started a part-time job handing out leaflets for N seconds. Eli- 1 wants to hand out as many leaflets as possible with her special ability, Cloning. Eli- gen can perform two kinds of actions below.
- Clone herself and generate Eli- (gen + 1) . (one Eli- gen (cloning) and one Eli- (gen + 1) (cloned) exist as a result of Eli-gen 's cloning.) This action takes gen \times C ( C is a coefficient related to cloning. ) seconds.
- Hand out one leaflet. This action takes one second regardress of the generation ( =gen ).
They can not hand out leaflets while cloning. Given N and C , find the maximum number of leaflets Eli- 1 and her clones can hand out in total modulo 1000000007 (= 10^9 + 7).
Constraints
- 1 \leq Q \leq 100000 = 10^5
- 1 \leq N_q \leq 100000 = 10^5
- 1 \leq C_q \leq 20000 = 2 \times 10^4
Input
The input is given from Standard Input in the following format:
Q N_1 C_1 : N_Q C_Q
The input consists of multiple test cases. On line 1 , Q that represents the number of test cases is given. Each test case is given on the next Q lines. For the test case q ( 1 \leq q \leq Q ) , N_q and C_q are given separated by a single space. N_q and C_q represent the working time and the coefficient related to cloning for test case q respectively.
Output
For each test case, Print the maximum number of leaflets Eli- 1 and her clones can hand out modulo 1000000007 ( = 10^9 + 7 ).
Partial Scores
30 points will be awarded for passing the test set satisfying the condition: Q = 1 .
Another 270 points will be awarded for passing the test set without addtional constraints and you can get 300 points in total.
Sample Input 1
2 20 8 20 12
Sample Output 1
24 20
For the first test case, while only 20 leaflets can be handed out without cloning, 24 leaflets can be handed out by cloning first and two people handing out12 leaflets each.
For the second test case, since two people can only hand out 8 leaflets each if Eli- 1 clones, she should hand out 20 leaflets without cloning.
Sample Input 2
1 20 3
Sample Output 2
67
One way of handing out 67 leaflets is like the following image. Each black line means cloning, and each red line means handing out.

This case satisfies the constraint of the partial score.
Sample Input 3
1 200 1
Sample Output 3
148322100
Note that the value modulo 1000000007 ( 10^9 + 7 ) must be printed.
This case satisfies the constraint of the partial score.