/
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
問題
E君は高校1年生。国立医大を目指して日々勉学にいそしんでいる。 そしてこの夏、彼は予備校に通って少しでも成績を上げたいと考えている。 しかしそんな彼は、勉学を妨げる重大な問題を抱えている。 それは知人の女子達がそれぞれ別に彼をデートに連れ出そうとしていることである。
Cさんとは幼馴染の間柄。肉料理が好物で、E君の手料理を食べ、毎日「大好き」「愛してる」とE君にべったりです。 Mさんとは偽装カップルの間柄。超美人な彼女は頻繁に悪い虫がよってくるので、E君を彼氏とすることで悪い虫を寄せ付けないようにしています。 Hさんとは先輩後輩の間柄。ひきこもりがちな彼女ではあるが、好きなマンガやアニメの趣味が合うE君のことに関してはとても積極的です。 Aさんとは幼きころ契りを交わした間柄。幼稚園のころの『こんいんとどけ』を大事に持っていて、ことあるごとに婚姻を強要してきます。
もし一人とデートに行くことになれば、後日デートに行かなかった女子一人一人とデートすることになりさらに彼の勉強時間は減っていく。
彼は恋愛アンチだ。学生が恋愛などというものに現を抜かすなど言語道断だと常々思っている。 過去1日27時間女子とのデートに人生を費やすという伝説の英雄Mr. TOKOSHIなる人物がいたらしいが、そんなものはもってのほかだ。
彼女達の行動を観察したところ、誰か一人と近い位置にいる場合、デートに連行されてしまう。 逆に、もっとも近い距離に二人以上いる場合はお互いを牽制しあって、連行されないことがわかった。 また、自宅と予備校の半径50m以内は淑女協定により連行されないらしい。 このことを利用して、E君はデートに連行されないルートを通り、予備校に通うことに決めた。 場合によっては予備校までのルート上に家屋が建っている可能性もあるが、 建物を飛び越えられる素敵なブーツを持ち合わせていないので、 ラーメンのお食事中にお邪魔することになったとしても、致し方ない。
明日からの予備校に備え、いざ就寝しようと思い、ふと問題に差し掛かった。 予備校に遅刻しないように家を出たいが、特殊なルートを通るため、通常のルート検索アプリでは移動時間を調べられない。 このままでは、めざましの時間を何時にセットすればよいか決められない。 あなたの仕事は、彼のために、女子に連行されずに予備校へ通うための最短ルートの移動距離を求めてあげることである。 移動距離が判明すればE君は自分の足の速さから移動時間を計算することができる。
入力
N EX EY SX SY GX_1 GY_1 : GX_N GY_N
- 1行目には整数 N が与えられます。
- N は女子の数を表します。
- 0 ≦ N ≦ 20 であることは保証されています。
- 2行目には整数 EX, EY が与えられます。
- EX はE君の X 座標を表します。
- EY はE君の Y 座標を表します。
- -1,000 ≦ EX, EY ≦ 1,000 であることは保証されています。
- 3行目には整数SX, SYが与えられます。
- SX は予備校の X 座標を表します。
- SY は予備校の Y 座標を表します。
- -1,000 ≦ SX,SY ≦ 1,000 であることは保証されています。
- 4行目から N+3 行目までの N 行では、女子の位置に関する整数 GX_i, GY_i がそれぞれ半角スペース区切りで与えられます。
- GX_i は i 番目の女子の X 座標を表します。
- GY_i は i 番目の女子の Y 座標を表します。
- -1,000 ≦ GX_i, GY_i ≦ 1,000 であることは保証されています。
- 位置の単位は全てメートルです。
- E君の自宅と女子の位置、予備校と女子の位置、女子の位置同士はそれぞれ異なることは保証されています。
出力
ルートが存在しない場合は
impossible とだけ出力せよ。移動距離が10,000を超える場合も
impossible とだけ出力せよ。出力の数値は10,000を超えない場合は絶対誤差が 10^{-6} 以下であれば許容される。
真の最短移動距離が 10,000 - 10^{-6} を超える場合でも
impossible とだけ出力することが許容される。
入力例
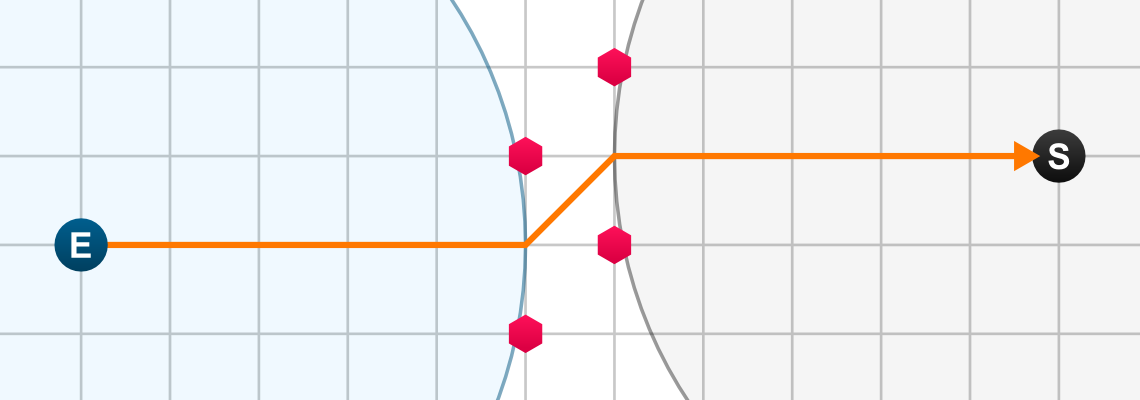
4 0 0 110 10 50 -10 50 10 60 0 60 20
出力例
114.142135623731
- 下図のようなルートを通るのが最善です。